Over the past year, I wrote a series of loosely related articles discussing the relationship of strength and muscle mass.
I’m realizing now that I wrote them completely out of order. This is the order they should have come out in, to introduce the concepts in a logical sequence.
- Who’s the Most Impressive Powerlifter to introduce the concept of allometric scaling and the difference between absolute strength and relative strength
- Strength vs. Size: How Important is Muscle Growth for Strength Gains to discuss the relationship between strength and muscle size in more depth,
- The Drug-Free Muscle and Strength Potential articles (one, two) to introduce the equations (based on muscle mass relative to height) that can be used to predict, quite accurately, strength potential for people who focus on powerlifting and are relatively gifted for the sport.
- How Much More Muscle Can You Build With Steroids to rigorously assess the advantage steroids give you for building muscle.
- This current article, to show the relative strength advantage you should expect to get from steroids.
- Steroids for Strength Sports: The Disappointing Truth to assess whether the predictions in this article, based on the equations presented and developed earlier in the series, actually play out in the real world.
However, I wrote them in almost the exact opposite order, so the first installment, which looked at the relative strength advantage provided by steroids, caused a bit of an uproar. This was partially my fault since I hadn’t provided enough context. To many people, the estimate that steroids provided a relative strength advantage of roughly 10% seemed like it simply had to be too low (though it was based on the best available data).
Couched in the context of the rest of this series, however, it’s easy enough to demonstrate mathematically that the advantage you’d expect, based on the current research, is somewhere in the neighborhood of 10%. That’s what I aim to do in this article to tie this series together and put a nice little bow on it.
If you’ve already read this series and you more-or-less understand all of the info and equations, you can just play around with the spreadsheet I made that does all the calculations for you. Otherwise, keep reading for a quick recap of this series and an explainer of the equations used to arrive at the prediction.
Absolute vs. Relative Strength
This is a key distinction and one that often gets lost in these discussions:
Absolute strength is simply the amount of weight you can lift. Relative strength is the amount of weight you can lift, relative to how large you are.
For example, if your squat goes from 500 to 550lbs, your absolute strength has increased without doubt. If it goes from 500 to 550lbs without a change in bodyweight, your relative strength has also increased. However, if your squat goes from 500 to 550lbs while your weight goes from 200 to 250lbs, your relative strength has decreased.
Relative strength is a thorny subject, because there’s no single agreed-upon way to assess it.
Strength to bodyweight ratios (i.e. squatting 2x bodyweight) are popular because they’re simple, but they’re not a great way to judge relative strength because they almost always favor lighter lifters. There are a lot more 150lb lifters who deadlift 450lbs than there are 250lb lifters who deadlift 750lbs.
Most powerlifting organizations use formulas like the Wilks formula or Glossbrenner formula to normalize relative strength performances and select the “best lifter” in a powerlifting meet. The Sinclair formula in weightlifting serves the same purpose. These formulas certainly do a better job than strength to bodyweight ratios, but I have some methodological quibbles with them. They’re not worth rehashing here, but you can read more about them in this article.
The scaling method I prefer for assessing relative strength is 2/3 power allometric scaling. This method of allometric scaling is based on the assumption that body mass scales linearly with body volume which is a third-order characteristic (which is a mathematically true relationship, assuming density – body composition in this case – remains constant), and strength scales linearly with muscle cross-sectional area which is a second-order characteristic (which may not always be true for people in the general population, but which seems to be true in the highly trained lifters for whom normalizing relative strength is important).
Regardless of the method you use to assess relative strength, the distinction between absolute and relative strength is an important one. Steroids certainly help you get stronger, but they primarily help you get stronger by helping you build more muscle. That muscle isn’t weightless, however, so the boost they provide for relative strength will be smaller than the boost they provide for absolute strength.
Predicting Strength Based on Jacked-ness
As discussed in these two articles (one, two), there is a very strong relationship between strength and fat-free mass per unit of height in elite powerlifters. Variation in FFM/cm can explain roughly 75% of the variability in bench and deadlift strength and almost 90% of the variability in squat strength.
Based on these relationships, we can use a simple regression equation to predict someone’s maximal strength capabilities based on how jacked they are: Powerlifting total (in kg) = 1563.9(FFM/cm)+77.32
So, for example, if someone’s 180cm tall and has 80kg of lean body mass, you’d expect them to total around 772kg (1700lbs) if they were a very skilled powerlifter.
Now, this formula doesn’t hit the nail on the head every time. Some people exceed the predictions if they’re exceptionally skilled lifters and very gifted for strength, and many people fall short of the predictions if they don’t train in a way that’s optimized for strength development or if they’re less gifted for strength development (and since the equation is based on high-level powerlifters, it is probably a bit too optimistic for a lot of people). However, it certainly does a good enough job to put us in the right ballpark for predicting maximal strength capabilities for a larger group of people when we’re dealing with averages.
How Much More Jacked Can You Get With Steroids?
For the long answer to this question, you can check out this article. But here’s the short version:
Fat-free mass index (a formula to normalize the amount of lean body mass you have relative to your height) is often used to assess human muscularity. The higher your FFMI, the more jacked you are.
The average untrained male has an FFMI around 18.9. With training, it seems the typical drug-free male ends up with an FFMI around 22.3, with a standard deviation of 1.9 FFMI points. On the other hand, the typical steroid user ends up with an FFMI around 25.5, with a standard deviation of 2.6 FFMI points, based on data from Kouri and Brennan.
In other words, the average steroid user gains roughly twice as much lean body mass over the course of a training career: 6.6 vs. 3.4 FFMI points. For an average-height male, that means the typical steroid user ends up with 10.4kg (23lbs) more lean body mass than a non-user.
Furthermore, the typical range of FFMIs for steroid users is larger than the typical FFMI range for non-users: 5.2FFMI points vs. 3.8 FFMI points (±1 standard deviation), meaning that as you get further from “average,” the gap between users and non-users grows. When you’re dealing with averages, the typical steroid user may be 3.2 FFMI points bigger and have 10.4kg more lean body mass, but by the time you get 3 standard deviations above the mean (i.e. where elite athletes would end up), steroid users have a 5.3 FFMI point advantage, corresponding with about 17kg (38lbs) more lean body mass for an average-height male.
In short, this should not come as a surprise to anyone, but steroids work really, really well for helping you build more muscle.
The Effects of Steroids on Relative Strength
Now that the stage has been set, we can predict the relative advantage afforded by steroids with some simple arithmetic using the data and formulae above. Click on the footnote to check my work. I’m just including all of the algebra so you can see I’m not using any mathematical sleights of hand. I’ll illustrate using allometric scaling to calculate relative strength.
1Basic formula:
(Allometric scaling score drug-free – allometric scaling score with steroids)/(allometric scaling score with steroids)
Expand the allometric scaling formula; Allometric scaling score = weight lifting × (body mass)-2/3
(Drug-free powerlifting total × (drug-free body mass)-2/3 – Powerlifting total with steroids × (body mass with steroids)-2/3)/(Powerlifting total with steroids × (body mass with steroids)-2/3)
Expand the formula used to predict strength; Powerlifting total (in kg) = 1563.9(FFM/cm)+77.32
((1563.9 × (Drug-free FFM/cm) + 77.32) × (drug-free body mass)-2/3 – (1563.9 × (FFM with drugs/cm) + 77.32) × (body mass with steroids)-2/3)/((1563.9 × (FFM with drugs/cm) + 77.32) × (body mass with steroids)-2/3)
Expand the body mass formulae; Normalized FFMI = FFM/(height in m)2 + 6.1 × (1.8 – height in m), so FFM = (FFMI – 6.1 × (1.8 – height in m)) × (height in m)2. Body mass = Lean body mass/(1 – body fat percentage)
((1563.9 × (((Drug-free FFMI – 6.1 × (1.8 – (cm/100)))*(cm/100)2)/cm) + 77.32) × (((Drug-free FFMI – 6.1 × (1.8 – (cm/100)))*(cm/100)2)/(1 – drug-free bodyfat percentage))-2/3 – (1563.9 × (((FFMI with steroids – 6.1 × (1.8 – (cm/100)))*(cm/100)2)/cm) + 77.32) × (((FFMI with steroids – 6.1 × (1.8 – (cm/100)))*(cm/100)2)/(1 – bodyfat percentage with steroids))-2/3)/((1563.9 × (((FFMI with steroids – 6.1 × (1.8 – (cm/100)))*(cm/100)2)/cm) + 77.32) × (((FFMI with steroids – 6.1 × (1.8 – (cm/100)))*(cm/100)2)/(1 – bodyfat percentage with steroids))-2/3))
Now allow for FFMI variability to account for standard deviations; FFMI = Mean FFMI ± (number of standard deviations × size of standard deviation)
((1563.9 × ((((mean drug-free FFMI ± (drug-free FFMI standard deviation × standard deviations from the mean)) – 6.1 × (1.8 – (cm/100)))*(cm/100)2)/cm) + 77.32) × (((((mean drug-free FFMI ± (drug-free FFMI standard deviation × standard deviations from the mean)) – 6.1 × (1.8 – (cm/100)))*(cm/100)2)/(1 – drug-free bodyfat percentage))-2/3 – (1563.9 × (((((mean FFMI with steroids ± (FFMI standard deviation with steroids × standard deviations from the mean)) – 6.1 × (1.8 – (cm/100)))*(cm/100)2)/cm) + 77.32) × (((((mean FFMI with steroids ± (FFMI standard deviation with steroids × standard deviations from the mean)) – 6.1 × (1.8 – (cm/100)))*(cm/100)2)/(1 – bodyfat percentage with steroids))-2/3)/((1563.9 × (((((mean FFMI with steroids ± (FFMI standard deviation with steroids × standard deviations from the mean)) – 6.1 × (1.8 – (cm/100)))*(cm/100)2)/cm) + 77.32) × (((((mean FFMI with steroids ± (FFMI standard deviation with steroids × standard deviations from the mean)) – 6.1 × (1.8 – (cm/100)))*(cm/100)2)/(1 – bodyfat percentage with steroids))-2/3))
The number it spits out will be negative, denoting the relative disadvantage of a drug-free athlete.
P.S. I’m almost certain there are too many parentheses above.
We can plug in height in cm, means and standard deviations for FFMI with and without steroids (based on Kouri and Brennan’s data, or your own assumptions), how many standard deviations from the mean you’re interested in (i.e. are you interested in the average advantage of steroids, or the advantage they give elite competitors), and the bodyfat percentages where you think someone would perform best on steroids and drug-free (since most people assume that steroids allow you to get leaner before performance is compromised), and this formula will predict the relative advantage steroids will give.
Assuming you don’t want to do all the math by hand, you can play around with this spreadsheet instead.
Let me walk you through it.
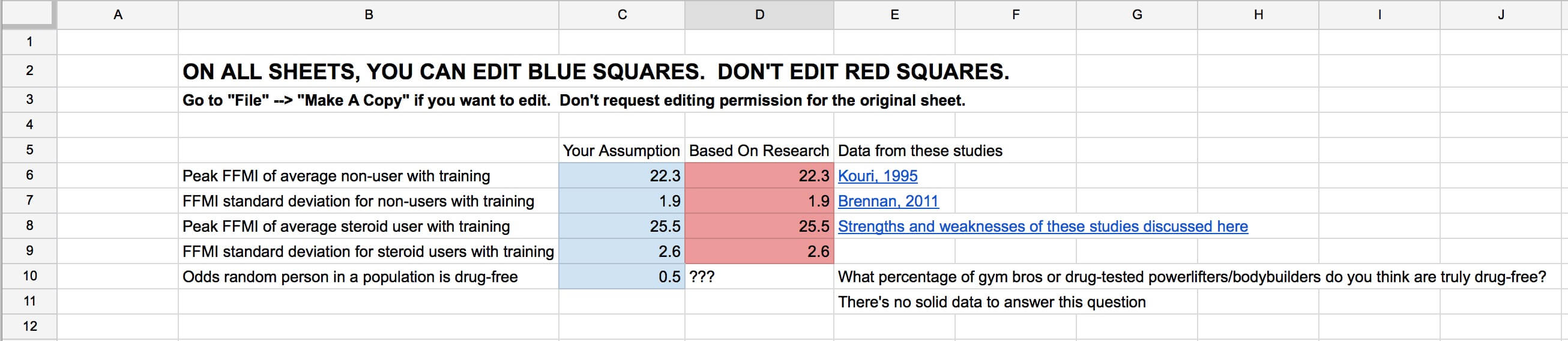
Page 1: Initial Assumptions
The numbers you enter on this page will substantially influence every other calculation.
The data entered in cells C6 through C10 are editable. The first four come filled-in based on the FFMI data provided by Kouri and Brennan, but you can play around with different assumptions to see how they affect the calculations. Cell C10 (odds a random person in a population is drug-free) is entirely up to you, and it affects the odds of someone’s natty-ness with a given FFMI on the third page.
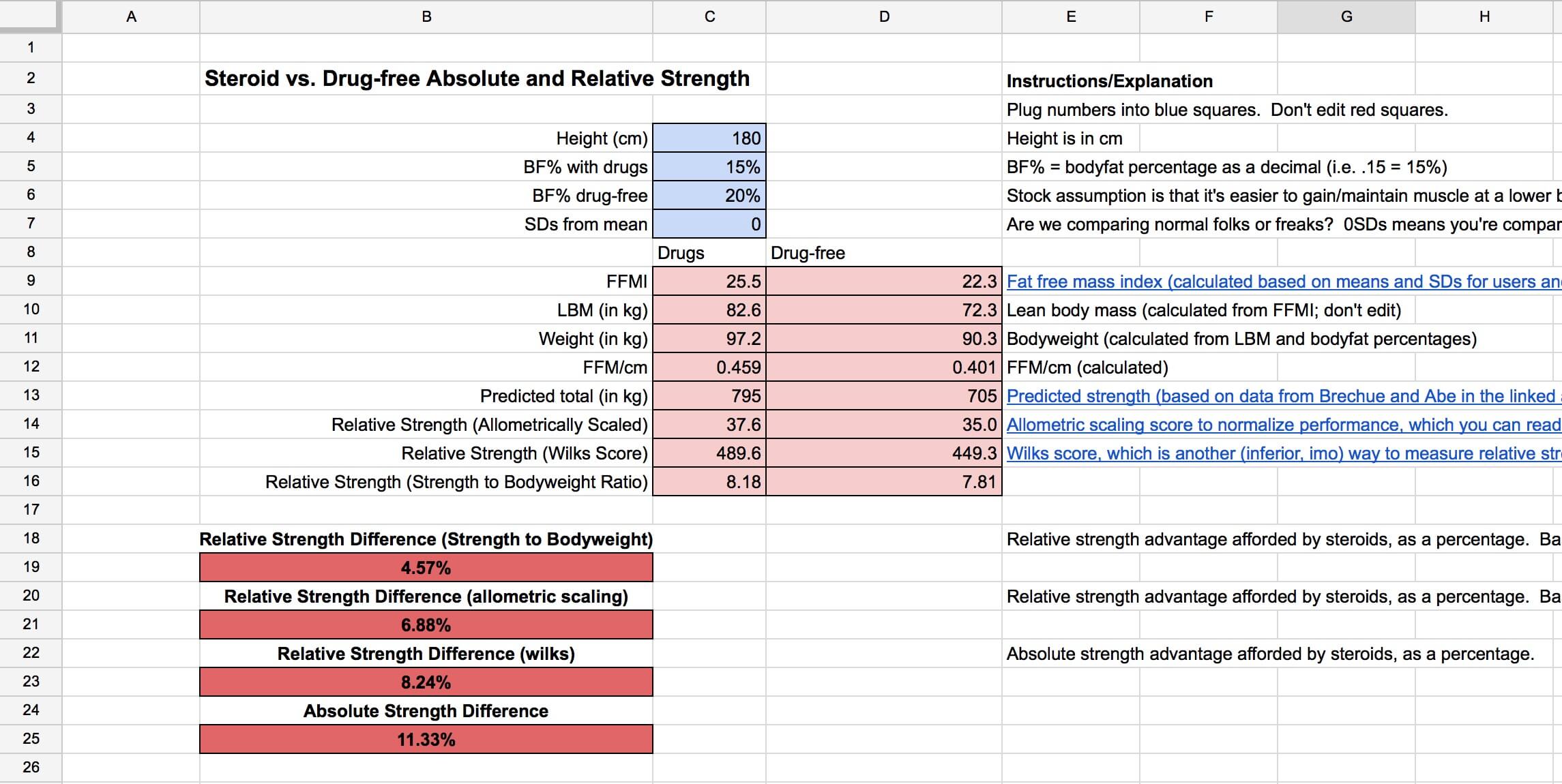
Page 2: Steroid Strength Advantage
This page does all of the really ugly algebraic calculations for you and shows you the differences in users and non-users every step of the way.
All you need to do is fill in cells C4 through C7, and it’ll do the rest.
This is fun to play with, I think. It seems taller people are afforded a larger advantage than shorter people. The assumptions you make about the differences in body fat percentage has a pretty large impact. If you assume steroids let people stay 10% leaner, the relative strength advantage is roughly 60% larger than if you assume steroids let people stay 5% leaner, for example. Finally, you can see how the advantage afforded by steroids gets progressively larger the further you get from the mean. The relative strength advantage is roughly 50% larger at 3-4 SDs from the mean versus 0 standard deviations from the mean.
Also note that the relative strength advantage is always smaller than the absolute strength advantage. This page also lets you see who’s advantaged and disadvantaged by each relative strength formula at various body weights. More muscle provides a larger allometric scaling benefit than Wilks benefit for lighter lifters, but the trend is reversed for taller/heavier lifters.
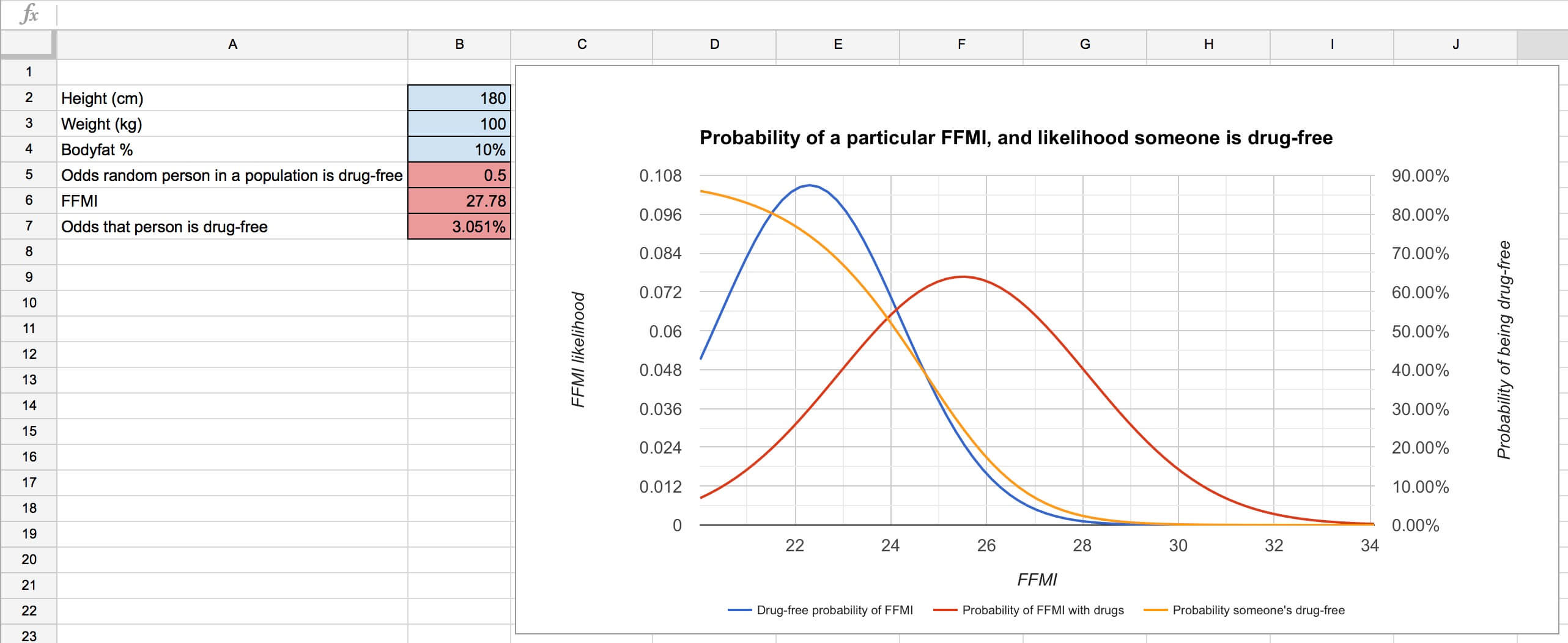
Page 3: Odds Someone Is Drug-Free
This page is an upgraded version of the tables near the end of this article.
It’s pretty simple. You fill in the blue squares, and the sheet calculates the FFMI based on the data you input. Then, based on some more simple math (probability density functions for FFMIs of users and non-users, based on the means and standard deviations of each population, weighted by your assumptions about the proportion of a population you think is actually drug-free), it tells you the probability that someone with such an FFMI is drug-free.
The blue curve is the odds of attaining a specific FFMI for a drug-free person, and the red curve is the odds of attaining a specific FFMI for someone on steroids. Both are weighted based on the percentage of the specific population you think is drug-free. For example, if you think 80% of the people in a given population are drug-free, it’ll make the blue curve bigger and the red curve smaller. The peak of the red curve is further to the right, denoting a higher average degree of muscularity for steroid-users, and there’s also more spread, denoting the larger standard deviation (potentially arising from differences in the compounds and dosages people use) for steroid-users’ FFMIs.
The yellow curve is the probability that someone with a given FFMI is drug-free (the likelihood is on the right y-axis). You see that where the blue curve is higher than the red curve, the probability is higher (indicating more drug-free people with a given FFMI), and where the red curve is higher than the blue curve, the probability is lower (indicating more steroid-users with a given FFMI). At the FFMI where the two curves intersect, the probability of someone being drug-free is 50/50.
The assumptions you start with on the first tab will affect this graph substantially – if you change the mean FFMIs for each group, that will shift the red and blue curves left or right. If you change the FFMI standard deviations, that will affect how spread-out the red and blue curves are. If you change the proportion of a population you think is drug-free, that’ll impact the overall size of each curve. All of these changes will affect the probability that someone with a given FFMI is drug-free (the yellow curve).
Perception = Reality. The Power of Confirmation Bias
This is where the rubber meets the road for this whole series.
Depending on the assumptions you start with, you can get any outcome you want from this spreadsheet. The first page (initial assumptions) determines how the rest of this sheet will behave.
If you go with the FFMI data from Brennan and Kouri (FFMIs of 22.3 ± 1.9 for non-users, and 25.5 ± 2.6 for users) and assume a steroid user can stay about 5% leaner than a non-user, you’d expect steroids to provide a relative strength advantage of roughly 7% for an average person, and around 11% for people 4SDs from the mean (averaging allometric scaling and Wilks).
If you start with the assumption that an FFMI of 25 is a hard limit for non-users (a common myth), then you’d expect a relative strength advantage of 16-17% 4 SDs from the mean. If you combine that assumption with the assumption that users can stay 10% leaner instead of 5%, and the relative strength advantage jumps to almost 20%.
Similarly, if you start with the assumption that 50% of drug-tested powerlifters or bodybuilders are lying about drug use, then based on Brennan and Kouri’s FFMI data, someone who’s 180cm tall, 90kg, and 10% bodyfat with an FFMI of exactly 25 would have a 33.7% chance of being drug-free. If you assume 95% of drug-tested athletes are actually drug-free, then this person would have a 90% chance of being drug-free. If you assume 80% of them are lying, however, his odds of being drug-free would be only 11%.
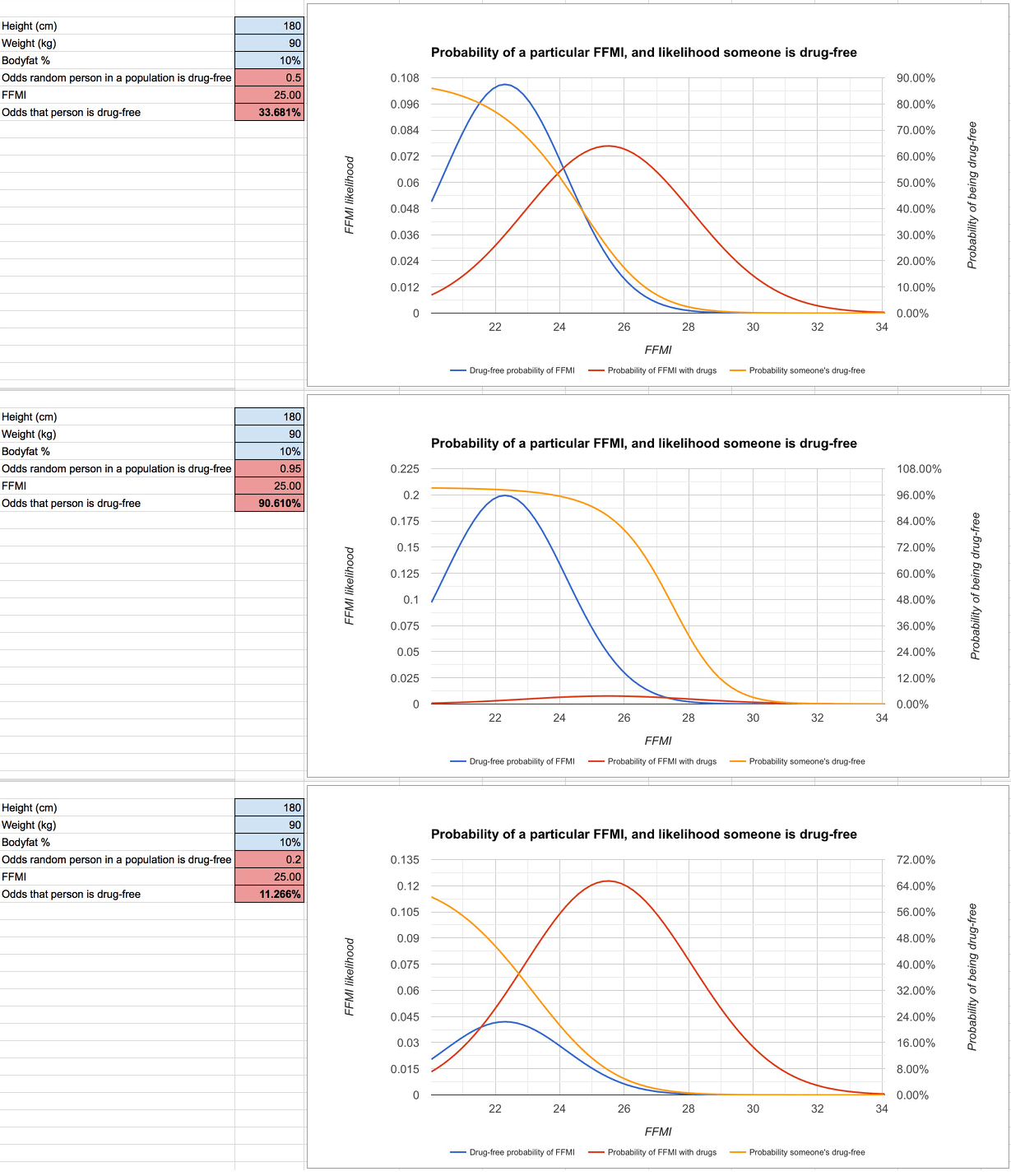
I think this is the fundamental reason why this is such a contentious subject. People come to this discussion with different sets of assumptions, and those assumptions alter their expectations. Those expectations affect how they interpret what they see (and even what data they’ll accept and what data they’ll reject), which further ingrains their biases. People who start with charitable assumptions about what drug-free athletes can accomplish and charitable assumptions about the proportion of drug-tested athletes who are actually drug-free are automatically labeled as naïve. Conversely, people who start with low assumptions about what drug-free athletes can accomplish and who assume most tested athletes are just cheaters who are beating the tests are automatically labeled as overly cynical.
This spreadsheet should show you how both “sides” can feel comfortable with their conclusions, based on differences in starting assumptions.
Bringing this series full-circle, the roughly 10% relative strength advantage from steroids proposed in this article seems to be a figure with experimental, observational, and (now) theoretical support. If you use Kouri and Brennan’s FFMI data, for most reasonable heights, body composition differences (0-10%), and distances from the mean (i.e. unless you project things out to 6+ standard deviations from the mean), the predicted relative strength advantage afforded by steroids tends to hover between 6-13% for both Wilks and Allometric Scaling.
If you disagree with the figure, there are a few ways you could dispute it:
- Provide better data showing average FFMIs for users and non-users.
- Show that the relationship between FFM/cm and strength is substantially different from the one found in Brechue and Abe’s work. Crucially, the strength increase for each increase in FFM would need to be larger than the one they found (a smaller increase per kg of FFM would decrease the predicted relative advantage of gaining FFM via steroids).
- Provide solid data showing that steroids increase strength independent of gains in muscle mass in elite athletes (i.e. that they raise the limit of attainable normalized muscle force, and don’t just potentially increase the rate of increase in untrained people). This is an idea I’ve seen floated before, but haven’t come across any solid data to support it.
Otherwise, I think it’s time to put a bow on this series for now.
Featured Image Credit: hookgrip