We’ve finally reached the end of this series that has spanned nearly four years. In the spring of 2016, we sent out a survey asking people a whole lot of questions about their training histories. Some of the most interesting data from that survey related to injury rates. We wrote that up, but recognized that the data from that survey was quite limited since it was purely cross-sectional. We then embarked on a year-long prospective study, following a group of (initially) 350 powerlifters over the course of a year in order to a) assess injury rates and b) see if we could see what factors increase or decrease injury risk in powerlifters. We’ve already provided an overview of the study, as well as the basic results. If you haven’t read the first two articles, you should check them out before diving into this one.
Now, this series is finally coming to a close. We’ll probably probe the data further (it also will let us examine what factors are associated with positive training outcomes, not just injuries), but this will sum up our examination of the injury data. In this article, we’ll be digging further into the data, and examining how the factors that may contribute to injury risk interact. We’re finally getting to the “answers” (or the closest we can come to answers) from this data set to the question: “What factors influence injury risk in powerlifters?”
As with our first two articles, we will go over the definition of acute injury we chose.
“Acute injury is defined as 1) any bone fracture, muscle/ligament/tendon tear, or joint sprain/dislocation/separation; 2) any injury that necessitated a trip to an MD or PT (not a chiropractor or massage therapist); 3) any injury of any variety that necessitated taking time off from training for two weeks or greater. For example, a knee injury that required you to stop squatting for three weeks even though you never stopped benching would be considered an acute injury. Being sore and skipping one workout would not be considered an injury.”
It’s important to understand why we chose this definition and how it might impact the results of the analysis. First, as this is a self-reported injury, the definition had to be easily understandable and broadly applicable regardless of level of medical professional involvement. We also wanted to ensure that a “significant training disruption” was the end result of the injury. Skipping one session or taking an extra day of rest is not truly a major disruption. Similarly, excluding chiropractor and massage therapist visits as an indicator of injury was meant to ensure that those individuals who routinely visit those providers as part of their recovery strategy would not be erroneously flagged as injured. Lastly, it must be noted that how strict this definition is will ultimately impact the rates or risk of injury. A definition of injury that is “something hurts” would result in nearly every lifter being injured (very high rates of injury), whereas one that required two separate confirmed radiological findings of a torn muscle, ligament, or broken bone would result in very few lifters at all being injured (very low rates of injury). Applying these two definitions to the same population would result in wildly different estimates for the exact same physical outcomes. Just keep in mind what we mean by injury when we say it, and what other publications or researchers mean when they say it.
Time
One of the challenging (and interesting) aspects of this study is how we handle time. The methodology for the analysis, known as survival analysis, is a pretty standard method for understanding time until event data, which in our case is injury. In a health care setting, a researcher might want to look at the survival of two groups of individuals following a heart transplant with Method A versus Method B. They would literally use the number of days since the transplant as the time variable. Both groups are exposed to “heart transplant” at all moments of time.
With lifting, time is slightly more involved, as the exposure (lifting) does not happen every day, so the individual cannot have a lifting-related injury every day. I (Andrew) generally lift about 4x per week, so over the course of a month, that’s about 17 days of training. If Greg lifts 2x per week, that’s 8.5 days of training. If we care about injury from lifting, I would have far more exposure to lifting than Greg over the course of 30 days, with about 9 more opportunities to get hurt.
Going even further, what if I only did 2 working sets each day, but Greg did 10 working sets per day? I’d have a total of 34 sets, whereas Greg had 85 sets, yielding much more lifting exposure on a per month basis. Theoretically, you could go even further into the nesting doll and break it out by reps as well.
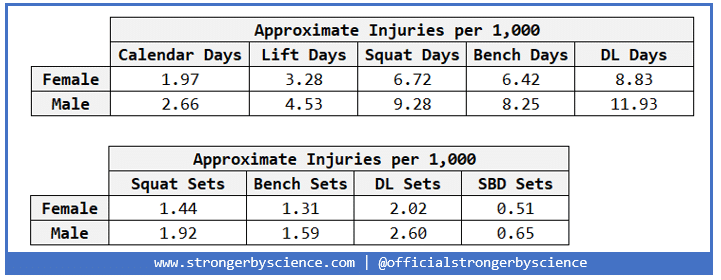
Table 1 presents the unadjusted injury rate data by calendar days, any lift days, and squat, bench, and deadlift days. Given that this is unadjusted for anything besides sex, I strongly discourage you from using this to make any conclusive or “proof” statements. Also, this is literally just counting, rather than a rigorous statistical method or test.
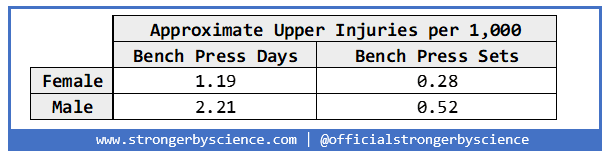
While this is certainly interesting and seems to hold with the idea from our first articles that men get injured slightly more often than women, there are substantive issues with this method of presenting the data broken out by lift. First off, while we have injury information by general body part, we do not know what lift caused the injury. While it is unlikely (although not impossible) that a lower body injury occurred while benching, upper and lower body injuries while squatting and deadlifting are both plausible. Table 2 uses exclusively upper body injuries and isolates bench press days and sets.
Again, we run into a problem where this has assumed that all upper body injuries are a result of benching, when we know that bicep, elbow, and shoulder injuries are all fairly common from squatting and pulling. Therefore, we will not be associating injury locations with lift type.
Modeling
As mentioned briefly above, the basic methodology for the statistical modeling portion of this analysis is called survival analysis or time-to-event. One of the most common tools for this work is called a Cox proportional hazard model1Cox, D. R. 1972. “Regression Models and Life Tables (with Discussion).” Journal of the Royal Statistical Society, Series B 34:187—220., and that is what we will be using. Briefly, the model will allow us to use multiple variables to understand the rate of an event (injury) at a point in time. The results of this model are what are known as hazard ratios for each variable in the model. Broadly speaking, hazard ratios can be interpreted as follows:
Hazard Ratio > 1: variable is positively associated with injury
Hazard Ratio = 1: no effect
Hazard Ratio < 1: variable is negatively associated with injury
Therefore, we will be able to use this model to look at the association of a set of variables with the injury outcome.
So far, everything presented has been unadjusted, univariate, or raw: mostly counts or proportions of data. Such representations are very useful for exploring the data, but less useful for meaningful analysis. Unadjusted results are the most simple way to present data but can be misleading or flat out wrong. For example, imagine that you have demographic information on 200 men for a study. You see an extremely statistically significant relationship between height and income and breathlessly report that with every 1” of height over 72”, the average income goes up by $500,000 a year. However, you did not control for the fact that you have 50 NBA players in your population. Once properly adjusted, it was found that while controlling for NBA status, there is no relationship between height and income.
However (and there’s always a however), just taking every single one of the 40+ variables collected and dumping them into a model, and then yelling that the model is adjusted for everything and is the Absolute Truth is also not exactly how it works. There is a decision making process ahead of time that needs to be done to determine what goes into the models. We believe that the following flowchart in Figure 1 generally represents our hypothesis regarding injury via training.
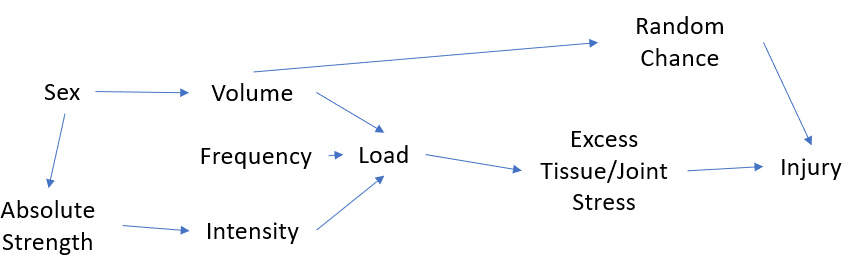
Therefore, we will include variables related to these processes. Additionally, we will not be picking and choosing after the fact; as discussed in Greg’s article about bad statistical practices or p-hacking, that is horrendous science. In addition to variables that impact training (as mentioned above), we will be sure to include/control for basic demographic information related to the individual.
Our initial model will be “time invariant” with regards to the variables – nothing changes, essentially. We collected information every month over the course of a year, but for a first attempt, we are only using information at baseline (first survey) to model injury risk. For example, a participant’s bodyweight and total will change over the course of a year, but we are ignoring that for now. This is the more basic of the two models, but not one without its merits. Table 3 presents the variables included in our first model2The model was a Cox proportional hazard model, and the proportional hazard assumption was checked and found to be appropriate. with values as baseline.
| Name | Type | Units | Values |
| Male | binary | – | Yes/No |
| Age | continuous | years | >= 18 |
| Height | continuous | inches | >= 54 |
| Bodyweight | continuous | pounds | > 90 |
| Limitations | binary | – | Yes/No |
| Total | continuous | 100 pounds | > 0 |
Time Invariant Model Results
The key phrase for these model results is “holding everything else equal.” What that means is that to understand the way that one variable impacts injury risk, you only change one variable at a time while keeping the others constant3This is the exact same coefficient interpretation strategy for multiple linear regression aside from the fact that these are exponentiated coefficients.. Using the height variable from Table 3 below, the interpretation of the model results is that for every 1” increase in height, the risk of injury decreases by 5%, based on its hazard ratio of 0.95 (95/100). For a binary variable such as sex, the interpretation is “being male increases risk of injury by 1.42-fold”.
| Variable | Units | Hazard Ratio | Significant | Meaningful |
| Height | inches | 0.95 (0.87-1.03) | No (p > 0.1) | No |
| Bodyweight | pounds | 0.99 (0.98-1.01) | No (p > 0.1) | No |
| Age | years | 1.01 (0.91-1.09) | No (p > 0.1) | No |
| Total | 100 pounds | 1.00 (0.99-1.00) | No (p > 0.1) | No |
| Limitations | Yes/No | 2.78 (1.73-4.47) | Yes (p = 2×10-5) | Yes |
| Sex | Male/Female | 1.42 (0.66-3.02) | No (p > 0.1) | Possibly |
What we see here parallels closely what we found in the first two articles. By far the strongest risk factor for injury is having a limitation at baseline. An example of that would be someone who has an older knee injury that limits their ability to fully hit optimal squat depth. The presence of these limitations yields a staggering hazard ratio of 2.78, indicating that those with limitations at baseline were nearly three times as likely to sustain a subsequent injury than those who did not start that study with any limitations. This was found to be highly significant and also highly meaningful (subject matter expertise based). The sex variable was not found to be significant, but is certainly something worth keeping an eye on given what we found in the pre-study analysis, the relatively high hazard ratio, and the male dominant study. Again, a reminder that p-values are not a hard and fast law from upon high about truth.
Obviously a lifter’s total, bodyweight, and style of training evolves over time. If we want to characterize injury risks, those should also be taken into consideration. Therefore, our next model will include “time varying” information, where there can be multiple measures for variables over time within the same person. If a participant started with a 1000lb total and added 10lb a month for 10 months, that participant would have 1000, 1010, 1020, etc., as their varying values for total. The same holds true for bodyweight and other variables that might change over time. However, the upside to the time-invariant model is that it can be used in a predictive manner of sorts4Not strictly a classical prediction model as there is no training, testing, validation, etc.. For example, in an applied situation, if you have five athletes under your care, and one is a male with a pre-existing limitation, it would be worth your time to possibly pay extra attention compared to four non-limited women.
Now, for a more comprehensive and realistic understanding of risk factors, we need to go to a time varying approach, or a multiple row per participant setup. Each individual will have all of their survey responses used, up to a maximum of 12 for someone who completed the full study uninjured.
Let’s go over what variables will be included in the time-varying model in Table 4.
| Name | Type | Units | Values | Time Varying |
| Male | binary | – | Yes/No | No |
| Age | continuous | years | >= 18 | No |
| Height | continuous | inches | >= 54 | No |
| Limitations | binary | – | Yes/No | No |
| Bodyweight | continuous | pounds | > 90 | Yes |
| Total | continuous | 100 pounds | > 0 | Yes |
| Days Cardio/Circuit Training per Week |
continuous | days | 0-7 | Yes |
| Days Lifted per Week | continuous | days | 0-7 | Yes |
| Squat Days per Week | continuous | days | 0-7 | Yes |
| Bench Days per Week | continuous | days | 0-7 | Yes |
| DL Days per Week | continuous | days | 0-7 | Yes |
| Squat Sets per Week | continuous | sets | >= 0 | Yes |
| Bench Sets per Week | continuous | sets | >= 0 | Yes |
| DL Sets per Week | continuous | sets | >= 0 | Yes |
| Percent of Squat Sets >85% | ordinal | % | 0%, 25%, 50%, 75%, 100% |
Yes |
| Percent of Bench Sets >85% | ordinal | % | 0%, 25%, 50%, 75%, 100% |
Yes |
| Percent of DL Sets >85% | ordinal | % | 0%, 25%, 50%, 75%, 100% |
Yes |
| Percent of Squat Sets >85% X Squat Sets per Day |
Interaction term | – | – | Yes |
| Percent of Bench Sets >85% X Bench Sets per Day |
Interaction term | – | – | Yes |
| Percent of DL Sets >85% X DL Sets per Day |
Interaction term | – | – | Yes |
Based on what we know about how we collected our data, the training process, and our injury hypothesis (Figure 1) we added some interaction terms into the model between the percent of sets over 85% and sets per day. Interaction terms allow us to test the idea that the relationship between the proportion of sets over 85% and injury risk varies by how many sets per day are performed.
As a reminder, all data is collected monthly, so “per week” is an estimate or average determined by the individual. Heavy was defined as greater than 85% of 1RM and was determined by the participant. The data that was collected did not get to the repetitions level, and we did not feel comfortable extrapolating to get there. Therefore, we acknowledge that there is a certain level of uncertainty with the volume estimates on a per set basis, but we believe that including the high intensity repetitions will help reduce the variance of that estimate. In general, this fits with our primary hypothesis that “doing too much” is the most important way to understand risk of injury (based on a combined many years lifting, coaching, and researching).
Time Varying Model Results
| Name | Units | Hazard Ratio | Significant | Meaningful |
| Male | – | 1.51 (0.79-2.85) | No (p > 0.1) | Possibly |
| Age | years | 1.01 (0.99-1.04) | No (p > 0.1) | No |
| Height | inches | 0.95 (0.88-1.01) | No (p > 0.1) | No |
| Limitations | – | 3.08 (2.07-4.56) | Yes (p < 0.001) |
Yes |
| Bodyweight | pounds | 1.00 (0.99-1.00) | No (p > 0.1) | No |
| Total | 100 pounds | 1.00 (0.99-1.00) | No (p > 0.1) | No |
| Days Cardio/Circuit Training per Week |
days | 0.92 (0.83-1.01) | Marginal (p = 0.091) |
Possibly |
| Days Lifted per Week | days | 0.97 (0.81-1.12) | No (p > 0.1) | No |
| Squat Days per Week | days | 1.17 (0.93-1.45) | No (p > 0.1) | No |
| Bench Days per Week | days | 1.13 (0.92-1.39) | No (p > 0.1) | No |
| DL Days per Week | days | 1.05 (0.81-1.38) | No (p > 0.1) | No |
| Squat Sets per Day | sets | 1.07 (0.81-1.41) | No (p > 0.1) | No |
| Bench Sets per Day | sets | 1.00 (0.77-1.30) | No (p > 0.1) | No |
| DL Sets per Day | sets | 1.00 (0.78-1.28) | No (p > 0.1) | No |
| Percent of Squat Sets >85% | % | 0.94 (0.41-2.2) | No (p > 0.1) | No |
| Percent of Bench Sets >85% | % | 1.16 (0.56-2.4) | No (p > 0.1) | No |
| Percent of DL Sets >85% | % | 1.27 (0.66-2.41) | No (p > 0.1) | No |
| Percent of Squat Sets >85% X Squat Sets per Day |
Interaction term | 0.93 (0.82-1.01) | No (p > 0.1) | No |
| Percent of Bench Sets > 85% X Bench Sets per Day |
Interaction term | 0.97 (0.84-1.15) | No (p > 0.1) | No |
| Percent of DL Sets >85% X DL Sets per Day |
Interaction term | 1.02 (0.90-1.12) | No (p > 0.1) | No |
Limitations
The biggest takeaway from the above Table 5 is that limitations is still a *gigantic* risk factor when you take into account the variables in Table 4/5 in a time varying manner. Of note, even the lower bound on the hazard ratio confidence interval is still 2.07, which in and of itself is huge. Also important: None of the baseline (time invariant) variables changed in significance or direction. That gives me confidence that the baseline model can be used as that loose prediction tool.
Cardio
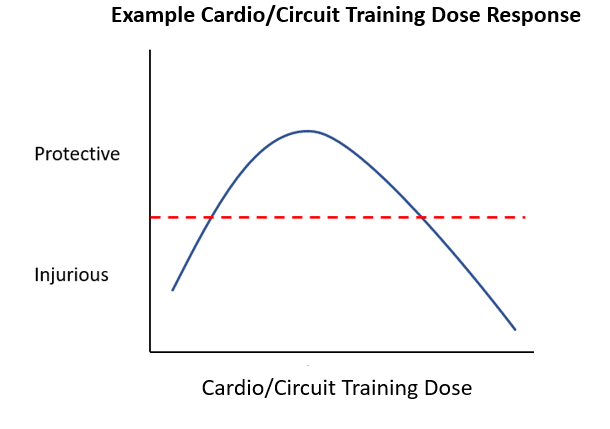
In a surprise to no one who actually understands how the body works, some participation in cardio or circuit training (which may include weightlifting components) is possibly indicated to be protective of injury. However, it is also likely that excessive amounts of these activities in addition to a standard amount of powerlifting training could exceed an individual’s maximum recoverable volume (MRV) in either the acute or chronic timescale, and could theoretically lead to injury. Figure 2 shows a likely example of how this relationship could work.
This is an oversimplified version of a dose-response curve in toxicology. Think of cardio like a prescribed medication, where the disease to be treated is powerlifting-related injury. Taking the prescribed amount (greater than zero) is beneficial, but taking too much (overdose) is possibly harmful. In terms of actual human health, regardless of powerlifting, you should be doing some element of regular exercise that challenges the cardiovascular system – hiking, CrossFit, basketball, whatever. You’ll set way more being alive PRs as a super-super masters lifter that way. Note that we weren’t looking for a non-linear relationship like this in our analyses, and the lifters in this sample weren’t also seven-day-per-week cardio bunnies. The actual analysis indicates that more days of conditioning work is protective, but since we weren’t studying lifters who also do a ton of cardio, we simply want to make clear that “more cardio is possibly protective” is likely only true to a point. As with anything, the dose (potentially) makes the poison.
Non-Significant Variables
It is extremely tempting when presenting results to only talk about the shiny low p-values. However, it is just as important to evaluate and interpret non-significant relationships as well. As mentioned previously, the fact that male trends to be a positive injury risk matters to me, despite its non-significant p-value. Our cross-sectional study found a strong positive relationship between male and injury, and the HR for male in this study was > 1.5 (CI: 0.79-2.85, p > 0.1). Although it was not statistically significant in the current study, this lack of statistical significance could be related to the small number of women as a percentage of the total sample or unmeasured/modeled confounders. Based on the findings of this analysis, combined with the cross-sectional results from the initial study and personal experience, I (Andrew) tend to believe that there is a real effect here that the statistical analysis was not able to accurately capture. Height, age, and bodyweight did not surprise me much but are important to control for nonetheless. I was surprised that the effect of powerlifting total was non-significant. Increased forces due to lifting occur with heavier weights and the stress tolerance of tissues does not necessarily increase in the same linear manner. It is possible, however, that the significance of the total would change if a substantially stronger population was studied. Further, survivorship bias could be at play, where those who were going to get hurt by getting strong are just more likely to wash out of the sport and not wind up in a study. It’s also possible that as lifters get stronger and more experienced, they also get savvier about their training, and learn how to better avoid injuries, despite (potentially) their increased strength.
It was also somewhat surprising that the days per week and sets per day variables were non-significant. One of the likely scenarios is that the lack of precision and accuracy in measuring exact volume figures essentially muddied the data in all directions, pushing results away from something meaningful5Non-differential exposure misclassification. Another is that in general, these training factors do not change that radically from individual to individual.
So What?
This was a fairly large amount of time and effort to come up with this recommendation: “Make sure you fully rehab injuries, so you’re not undertaking strenuous training while dealing with significant pre-existing limitations.” Welcome to conducting research. Not every study conducted has conclusions worthy of the front page of Nature, but that’s exactly the point. Science is a cumulative process with iterative improvements on the work of others that eventually leads to breakthroughs. You should not ascribe value to good faith research exclusively based on the presence or absence of a flashy, totally novel result. Building the body of knowledge and generating additional hypotheses and avenues of inquiry is absolutely vital to the general scientific community.