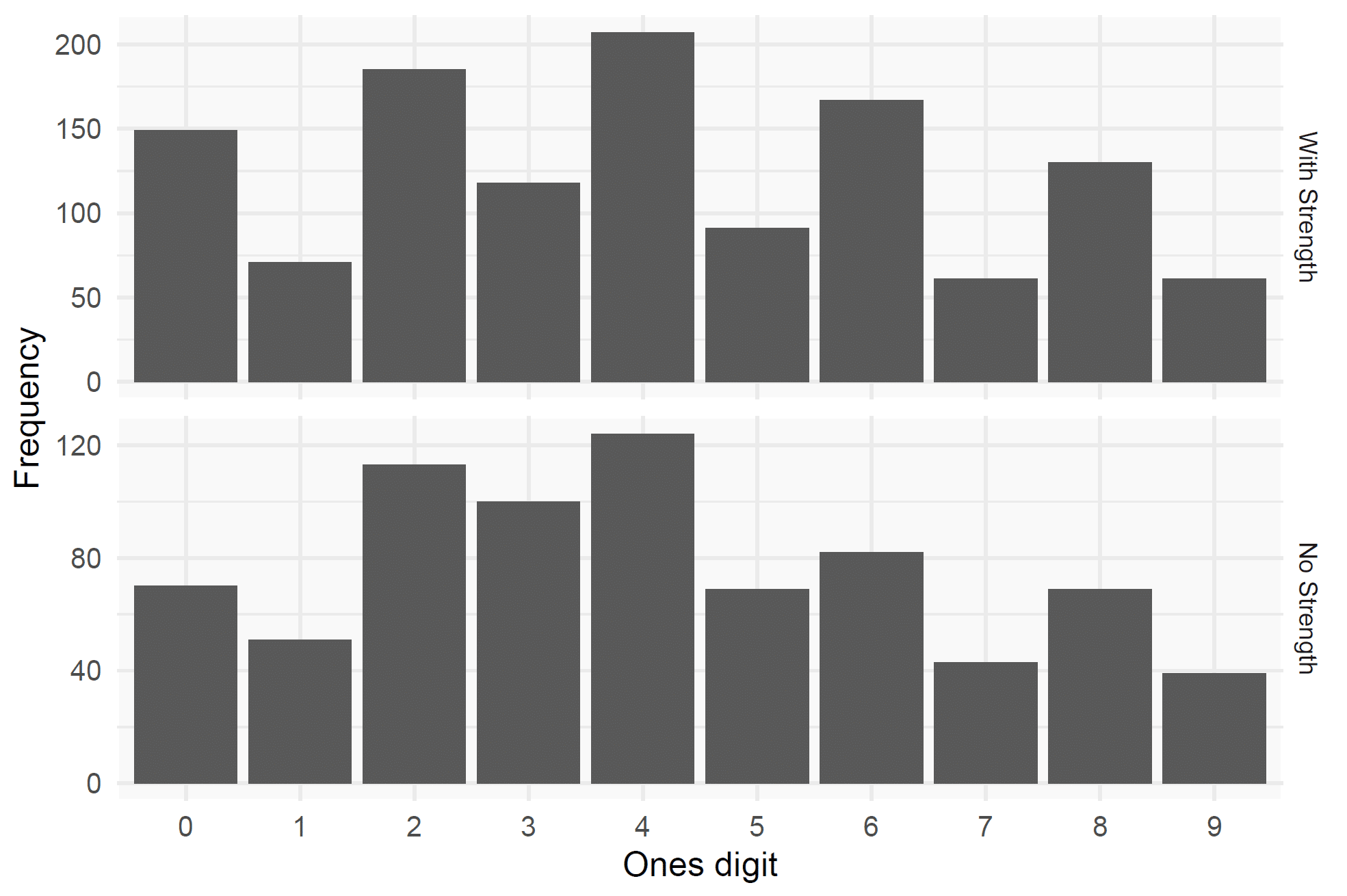Yesterday, a group I’m a part of published a white paper highlighting unusual data patterns in the research of Matheus Barbalho. You may have seen it already, or this may be the first you’re hearing about it. If you haven’t at least perused it, you should take a peek. My goal is for this article to serve as a more reader-friendly version of the white paper, and to give a little more context about this whole situation.
First, though, let’s back up a few steps. Who is Matheus Barbalho, and what’s all the hubbub about in the first place?
Barbalho is a graduate student from Brazil who does sports science research. His more well-known studies have focused on the effects of training volume on muscle growth and strength gains, and the effects of single- vs. multi-joint training. I am not throwing any accusations around in this article, but a group of researchers (and me) find some of the data patterns in Barbalho’s research to be highly unlikely.
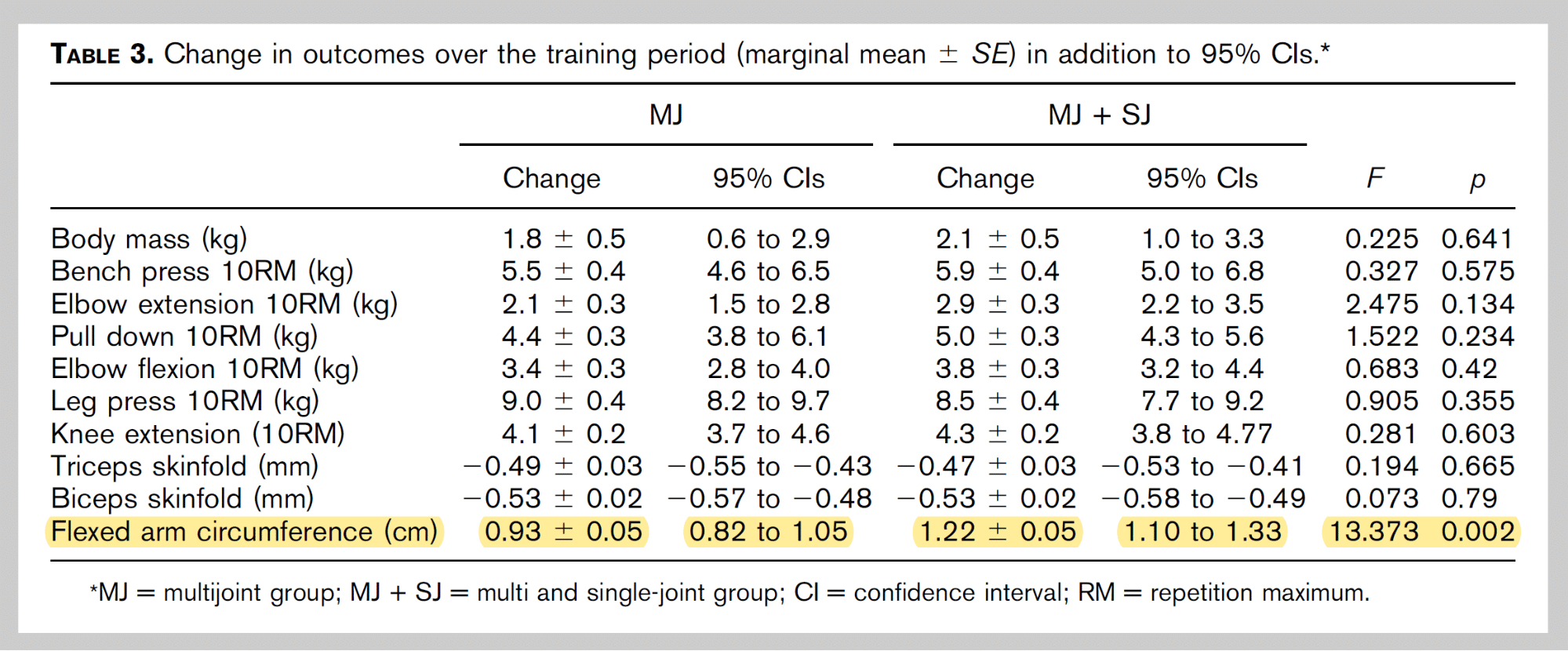
Before digging into the actual data, I want to give some personal context for this whole situation, just to explain why I started looking into Barbalho’s work in the first place. This may feel sudden, but the first time I noticed atypical results in his research came back in June of 2018 when I first read this study. One group of untrained female subjects increased their flexed arm circumference by 0.93cm, and the other group increased their flexed arm circumference by 1.22cm. This was a statistically significant difference. The fact that a difference of 3 millimeters ended up being statistically significant was a little surprising, but the absurdly low p-value (p = 0.002) was even more surprising. The low p-value was a result of the changes in both groups being incredibly consistent. But hey, weird stuff happens in research sometimes. I noted it as an odd little anomaly, and then mostly forgot about it.
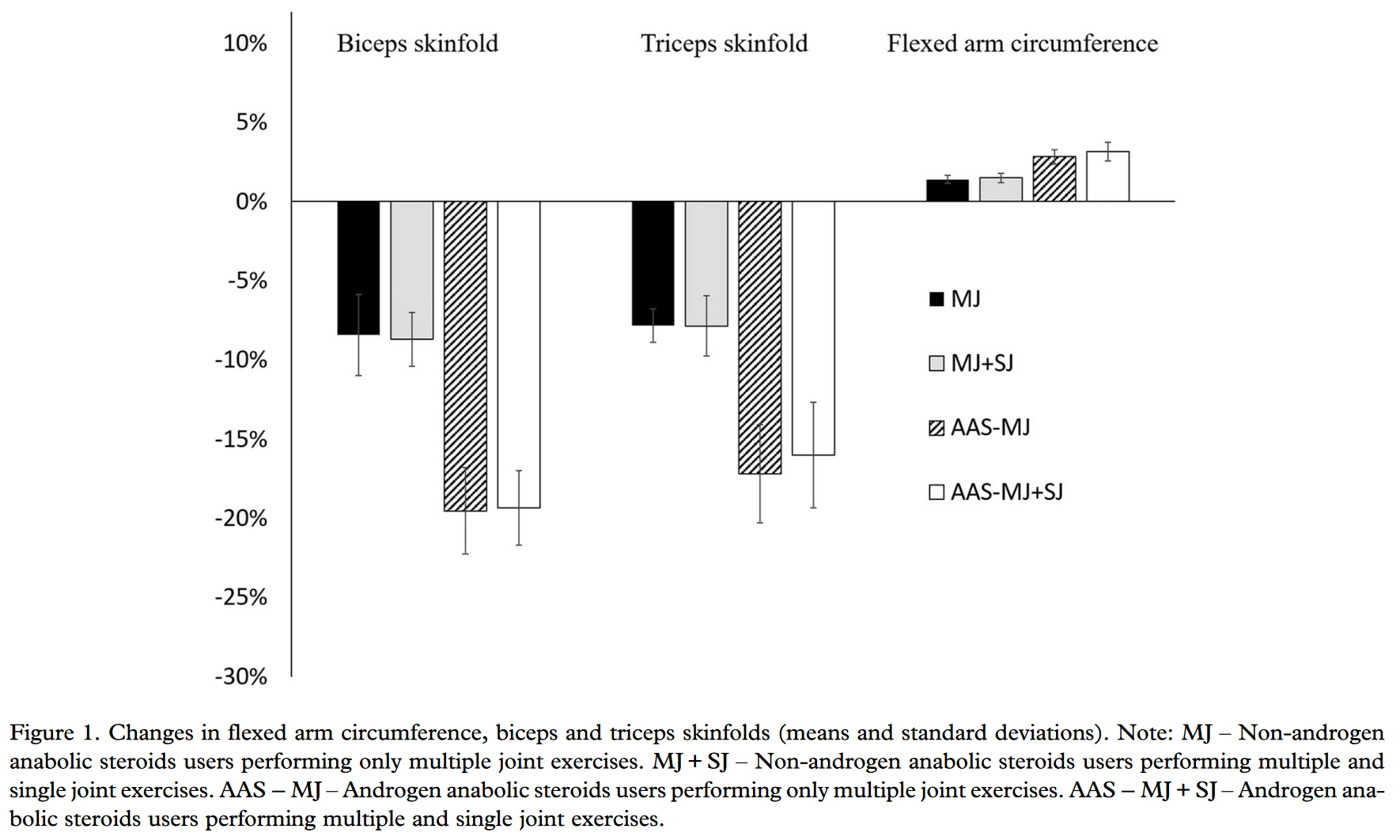
Almost exactly a year later, I was reading this study, and I once again noticed some confusing details. It compared two groups of bodybuilders who used steroids, and two groups of bodybuilders who were drug-free. Strangely, all four groups had almost identical baseline measurements across all variables, which seemed odd, since steroids tend to help people gain strength and build considerably more muscle. It certainly seemed like the steroid groups were doing their first cycle during the study (which isn’t how it sounds in the text of the study). But, “oh well,” I thought, “it’s pretty common for ‘subjects’ and ‘methods’ sections to contain insufficient information. Maybe they just excluded that detail.” Another thing that struck me was the standard deviation bars on the bar graph showing changes in flexed arm circumference. The standard deviations were only ~0.25% for the two drug-free groups, and ~0.5% for the steroid groups.
Again, that’s absurdly small, and implies that all subjects in each group got outrageously consistent results. This was also the first study by Barbalho where I realized how small all of the standard deviations were. For example, 10RM leg press strength in all of the groups was ~172kg at baseline, with standard deviations of just 2.2-4.5kg. That implies that all of the baseline leg press 10RMs fell within a ~15-20kg range. That’s a much, much tighter range than I’m used to seeing in other studies. By this point, I was starting to grow more skeptical.
Finally, this study was the one that finally prompted me to look into Barbalho’s body of work more closely. In this study, groups of strength-trained women completed a program of either squats or hip thrusts for 12 weeks. While people were focused on the flashy result (“squats build the glutes better than hip thrusts do!”), I was immediately drawn to the strength gains in the squat group. Their 1RM back squat (to full depth; 140 degrees of knee flexion) increased from 91.9 to 124.9kg in three months, at an average body mass of 69.5kg. As of the time of writing, a 91.9kg squat in the 72kg class in drug-free powerlifting would make a female lifter a 15th percentile squatter. A 124.9kg squat would rank them in the 65th percentile. That’s an astounding jump in three months. And all from six sets of squats to failure, once per week? I’d certainly never claim that such an increase is literally impossible, but adding 33kg in three months as a group average seemed incredibly high. When I searched Barbalho’s name on PubMed and realized I’d observed some atypical results in two prior studies he’d authored, that was enough to warrant a closer look. I also felt somewhat obligated to look closer, because I’d previously written about and discussed Barbalho’s research approvingly, so I felt the need to see whether I’d potentially done my audience a disservice.
Around the same time, Andrew Vigotsky messaged me about the squat vs. hip thrust study, because he was also surprised by the strength gains in the squat vs. hip thrust study. We started looking into some of the findings and found some things that deepened our suspicions, so I hit up James Heathers (who you may know from hits like, “boy oh boy, Brian Wansink’s research sure seems fishy”) for some guidance on how to proceed. James Krieger and Brad Schoenfeld had also messaged Andrew and me about some other concerns they’d had. I got all of us together in a group chat, and we started digging. Pretty soon, we’d uncovered several anomalies that warranted a closer look. As the number of statistical oddities began to grow, Andrew reached out to his friend James Steele, who was one of Barbalho’s frequent collaborators. Once James Steele joined our merry band, with access to some of the raw datasets, things really took off. Andrew and I started the process of analyzing the data in late January, and the wider collaboration got rolling on February 3, so we’ve been hard at work for almost 6 months now.
Before breaking down our findings, I think it’s important to lay out the timeline of events, just so you can see we’ve tried to be as above-board as possible.
Mr. Barbalho is Dr. Paulo Gentil’s student, so we notified Dr. Gentil about our initial findings on February 11, so Mr. Barbalho and Dr. Gentil have been aware of many of our concerns for approximately five months.
We sent Dr. Gentil the first version of the white paper on March 26, asking for an explanation or rebuttal by April 10. Mr. Barbalho asked for an extension to April 17.
On April 15, they informed us that the data in one of the studies was incorrect, and they subsequently (April 17) requested that the paper be retracted (it has now been retracted). The authors state that the study was carried out as described, but the undergraduate student who was responsible for transferring the data from paper to Excel “made much of the data” because he was “too busy to do the job.” However, our concerns extend well beyond that one paper, and we still had not received an explanation or rebuttal for our other concerns.
At this point, we contacted Mr. Barbalho, Dr. Gentil, and the other coauthors on the studies we had concerns about, asking if they’d support the publication of the white paper, retractions or, at minimum, for the journals to place expressions of concern on the studies. One of the coauthors (Dr. Jurgen Giessing) was receptive, but others were not.
Some of the coauthors had suggested that the appropriate course of action would be to attempt to resolve these issues through the journals in which they were published, so we contacted the journal editors on June 10. One of the journals (Experimental Gerontology) followed up with Dr. Gentil; Dr. Gentil responded, and discussions with that journal are ongoing. The rest of the journal editors mostly agreed that they’d like us to attempt to resolve the issues with Mr. Barbalho and Dr. Gentil again.
So, on June 22, we once again emailed Mr. Barbalho, Dr. Gentil, and the other coauthors, asking for explanations about the anomalous data patterns we’d observed. We gave them a three-week deadline, which expired at 11:59PM on July 13. We did not receive any response.
Hence, on July 14, we requested retraction of the seven remaining papers (the nine listed below, minus the one that’s already been retracted, and the one published in Experimental Gerontology), and we’re pre-printing the white paper to make the broader research community aware of our concerns.
Finally, I just want to reiterate: we’re not trying to levy any accusations. The data simply are atypical, improbable, and to put it bluntly, pretty weird. And if they’re weird for totally explainable and innocent reasons, we’re open to hearing those reasons. We just haven’t been presented with an adequate explanation yet.
Findings
In this section, I’ll be going through the white paper, and attempting to explain our findings in terms that virtually anyone can understand if they’re willing to invest a little time and focus. The white paper itself is a technical document intended for academics with some degree of formal statistics training, so it’s totally fine if you don’t understand parts of it. My goal is for this article to be understandable, even if you’re not super conversant in statistics (though, to give you fair warning, it will be pretty dense). I’ll try to teach you what you need to know as we go along. Also note, I won’t be following the white paper point-by-point. This article is organized so that broad critiques based on summary data (i.e. what all of you would have access to) are presented first so that you can see the sorts of things that encouraged us to keep digging deeper. Next, I’ll cover the critiques presented in the white paper that relate to the raw data in specific studies (i.e. data you don’t have access to). I’ll finish the first version of this article with further observations about Barbalho’s research that are worth mentioning, but didn’t warrant inclusion in the white paper. If we uncover any new anomalies, or if there are any major developments, I’ll add addenda to this article to keep it up-to-date.
Below is a list of Barbalho’s studies that we examined. With one exception, these were the studies we focused on because they’re the studies most relevant to the niche we’re all focused on: muscle growth and strength development. The one exception is the volume study on elderly women. You’ll see why we included it later on.
- The Effects of Resistance Exercise Selection on Muscle Size and Strength in Trained Women.
- Back Squat vs. Hip Thrust Resistance-training Programs in Well-trained Women.
- Evidence of a Ceiling Effect for Training Volume in Muscle Hypertrophy and Strength in Trained Men – Less is More?
- Single joint exercises do not provide benefits in performance and anthropometric changes in recreational bodybuilders.
- Evidence for an Upper Threshold for Resistance Training Volume in Trained Women.
- Does the addition of single joint exercises to a resistance training program improve changes in performance and anthropometric measures in untrained men?
- Effects of Adding Single Joint Exercises to a Resistance Training Programme in Trained Women.
- Influence of Adding Single-Joint Exercise to a Multijoint Resistance Training Program in Untrained Young Women.
- There are no no-responders to low or high resistance training volumes among older women.
Findings Based on Summary Data
Variances and Coefficients of Variation
To understand this section, it’s important to understand four concepts: S-values, standard deviations, coefficients of variation, and correlation coefficients.
S-values are like a more intuitive cousin of the p-value. An S-value tells you how surprising a finding is, and it lends itself to a simple analogy: flipping a fair coin. An S-value of 4 means a particular finding is about as surprising as flipping a fair coin and getting “heads” four times in a row; an S-value of 4 is pretty similar to the “traditional” p-value significance threshold of p=0.05. A higher S-value means a finding is more surprising. An S-value of 10 is similar to getting 10 heads in a row, and is comparable to a very low p-value of 0.001. An S-value of 20 is similar to getting 20 heads in a row, and is comparable to an incredibly low p-value of .000001. Note that an S-value tells you how surprisingly different two things are if you assume those two things should be similar. So, a high S-value may not necessarily indicate that a difference is particularly surprising, if it’s unreasonable to assume that two things should be similar. For example, if you compare the baseline body weights of two groups of randomly assigned, resistance-trained males, a high S-value is fairly surprising. If you compare the body weights of a group of elephants to a group of mice, a high S-value isn’t surprising at all.
A standard deviation tells you, “how spread out are the data?” About two-thirds of your data should fall within one standard deviation of your mean (average), about 95% of your data should fall within two standard deviations of your mean, and 99.9% of your data should fall within three standard deviations of your mean (assuming your data approximate a normal distribution). So, if a group of subjects bench press 100 ± 10kg, the mean is 100kg, about two-thirds of people should bench press 90-110kg, about 95% of people should bench press 80-120kg, and virtually everyone in your sample should bench press 70-130kg.
A coefficient of variation tells you, “how spread out are data, relative to the mean?” You calculate the coefficient of variation by dividing the standard deviation by the mean. So, if a group of people bench presses 100 ± 10kg, and squats 200 ± 20kg, the standard deviation is larger for the squat (20kg vs. 10kg), but the coefficients of variation are the same (10/100 = 10%, and 20/200 = 10%). In both cases, about two-thirds of the data will be within 10% above or below the mean, about 95% will be within 20% above or below the mean, and virtually all of the data should be within 30% above or below the mean. If, on the other hand, these individuals squatted 200 ± 10kg, the standard deviation would be the same for both the bench and the squat, but the coefficient of variation would be smaller for the squat (10/200 = 5%).
Correlation coefficients tell you, “when one variable changes, how predictably does another variable change, and in what direction does it change?” A correlation coefficient close to 1.0 indicates that when one variable increases, another variable increases in a very predictable fashion. As positive correlation coefficients get closer to 0, that tells you that when one variable increases, another variable also increases, though in a less predictable manner. A correlation coefficient of 0 tells you that there’s no relationship between two variables – when one variable changes, the other variable either doesn’t change at all, or it changes in a completely unpredictable fashion (assuming you chose the correct form of regression). A negative correlation coefficient close to -1.0 indicates that when one variable increases, another variable decreases in a very predictable fashion. As negative correlation coefficients get closer to 0, that tells you that when one variable increases, another variable decreases, though in a less predictable manner.
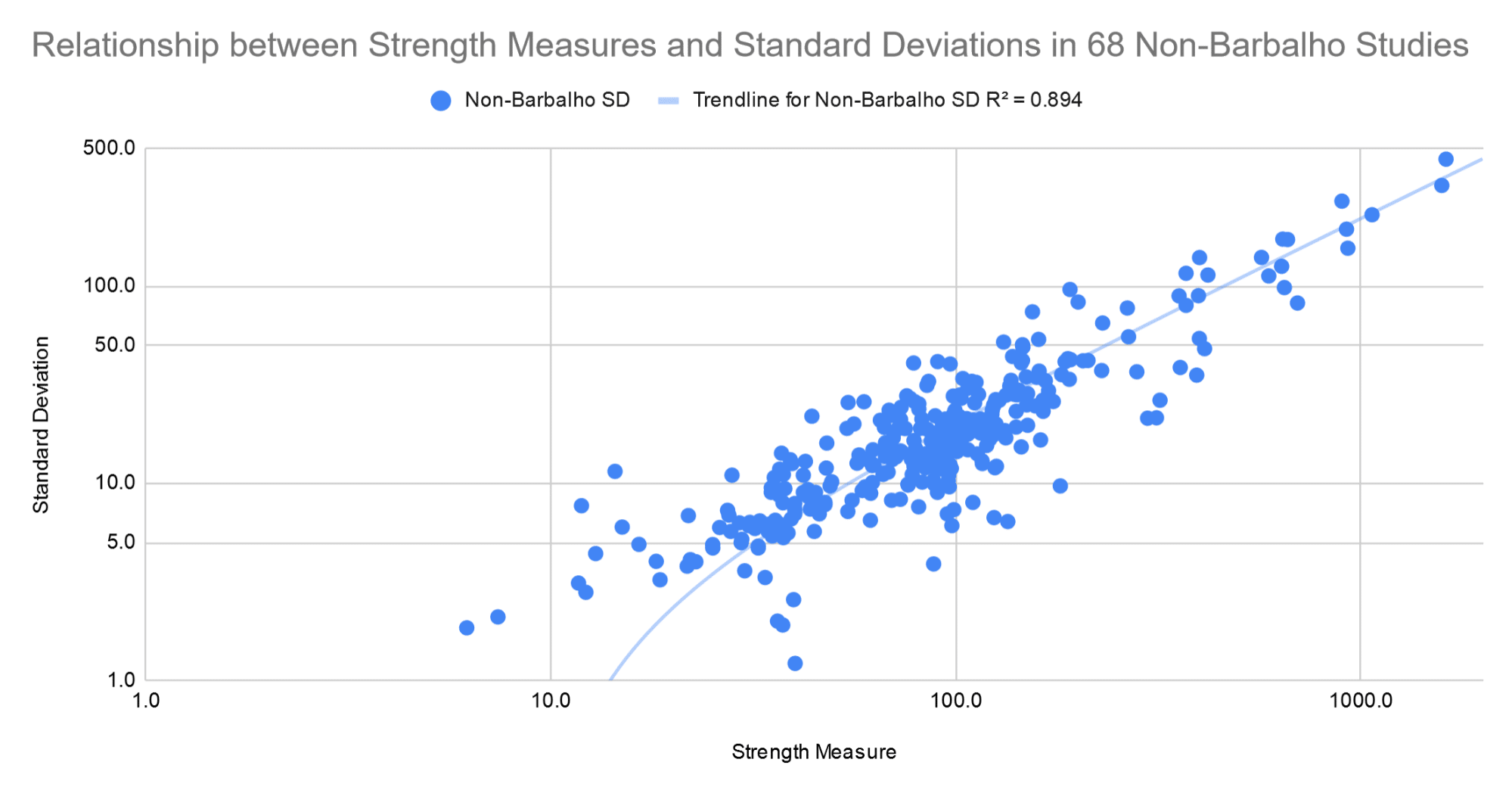
In general, as means get larger, standard deviations get larger too. I’ve done a few off-label meta-analyses on this site before (one, two, three, four), and we used the studies included in those articles as our proxy for the literature as a whole. There were 68 studies on young, healthy subjects with a combined 300+ strength measures (you can find citations for all of these studies in the white paper). These studies covered sex differences in resistance training, periodized vs. non-periodized training, and the impact of frequency on hypertrophy and strength gains, so this sample of studies covers a pretty broad swath of the resistance training literature. We used this set of pre-collected studies to reduce the risk of bias in selecting a group of studies to compare Barbalho’s results against.
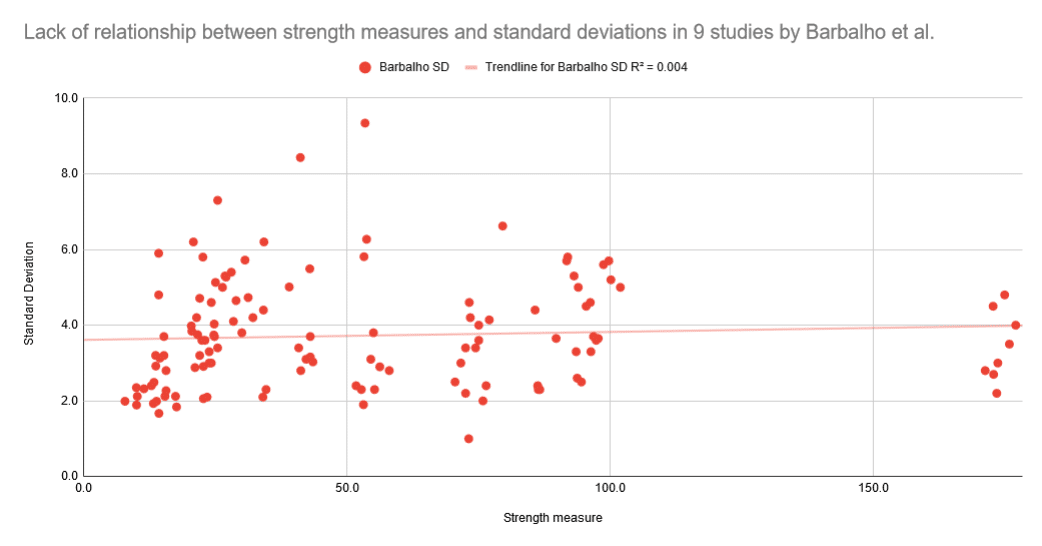
Here, you can see the relationship between mean strength measures (x-axis), and corresponding standard deviations (y-axis) in these studies. Note that the axes are log-scaled so that you can see all of the data points more clearly.
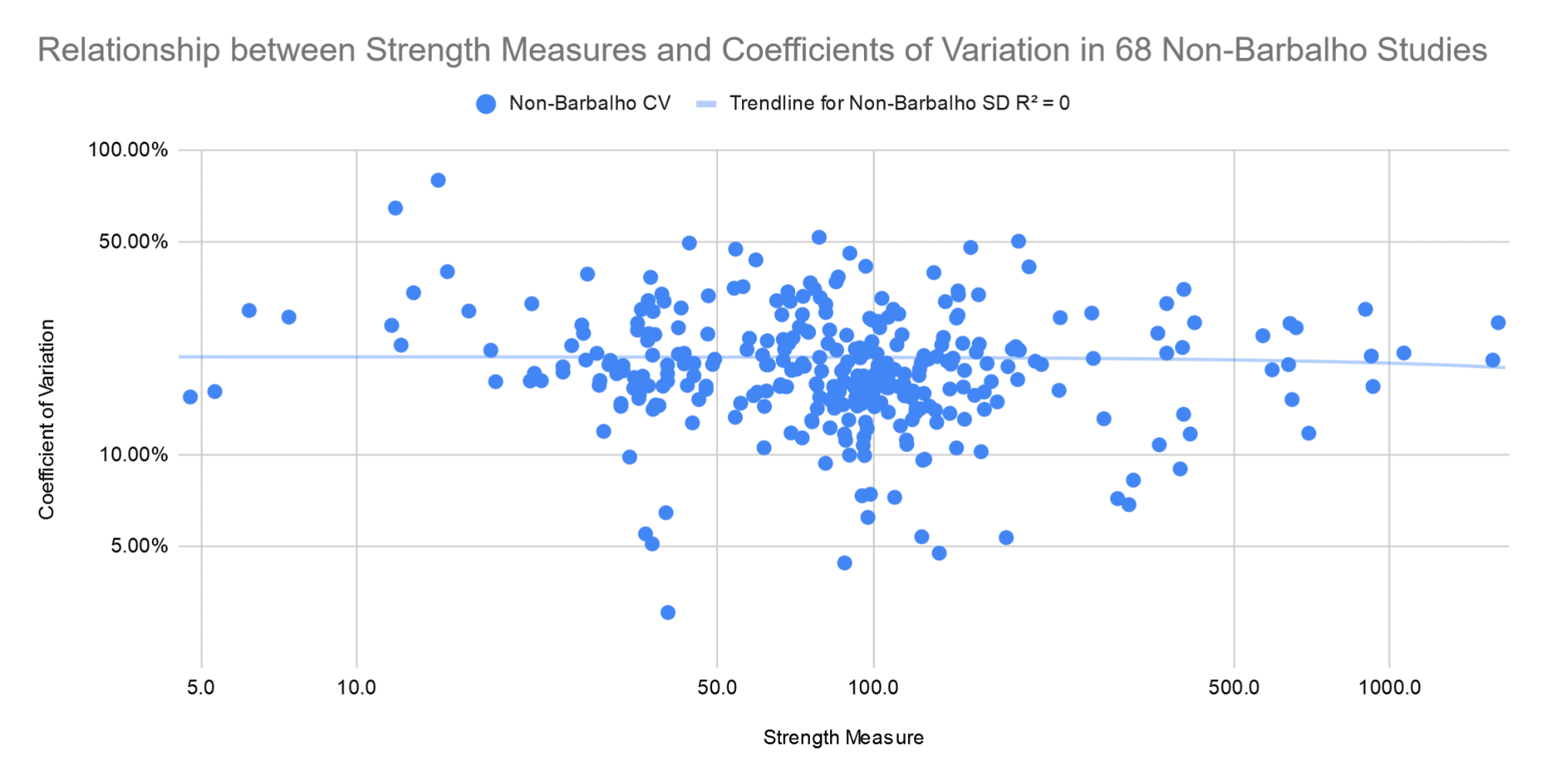
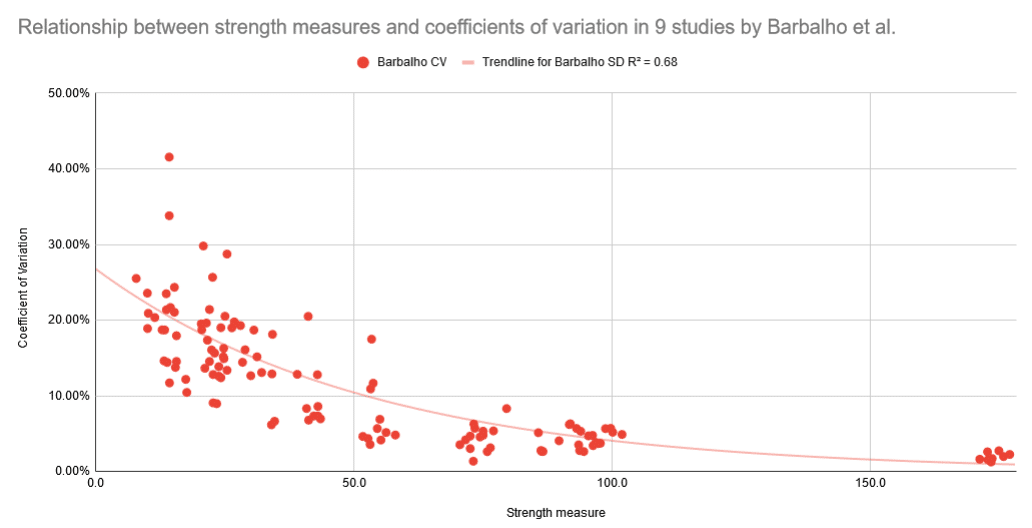
As you can see, standard deviations increase linearly as means increase. The relationship is very consistent (R = 0.946). As a result, coefficients of variation aren’t affected by mean strength. They’re generally somewhere between 12% and 30%, regardless of whether the study includes people curling 15kg, or leg pressing 400kg. On this graph, the axes are log-scaled again (again, to show the data more clearly).
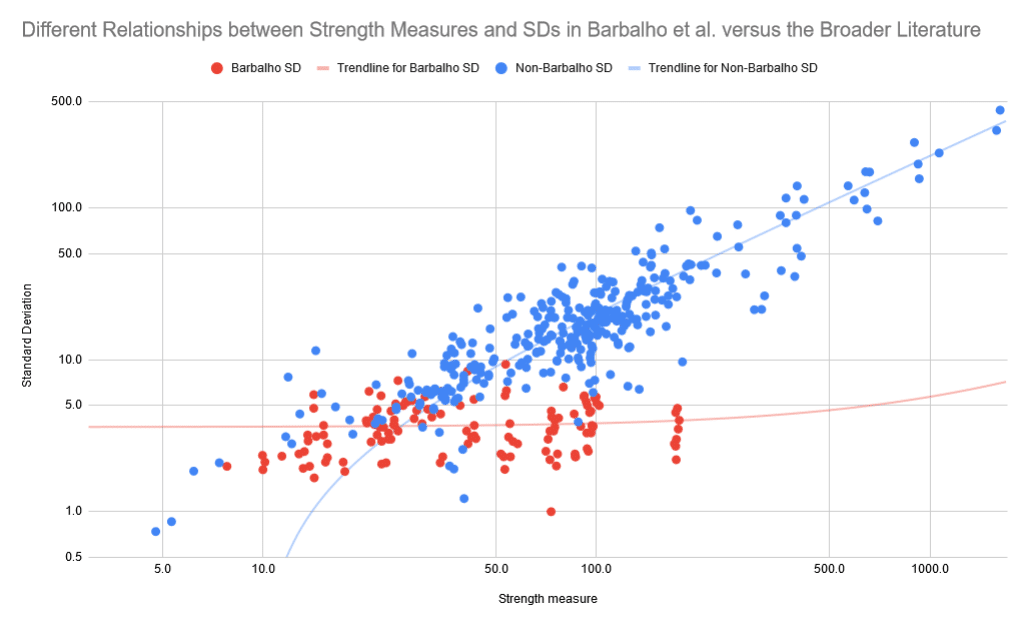
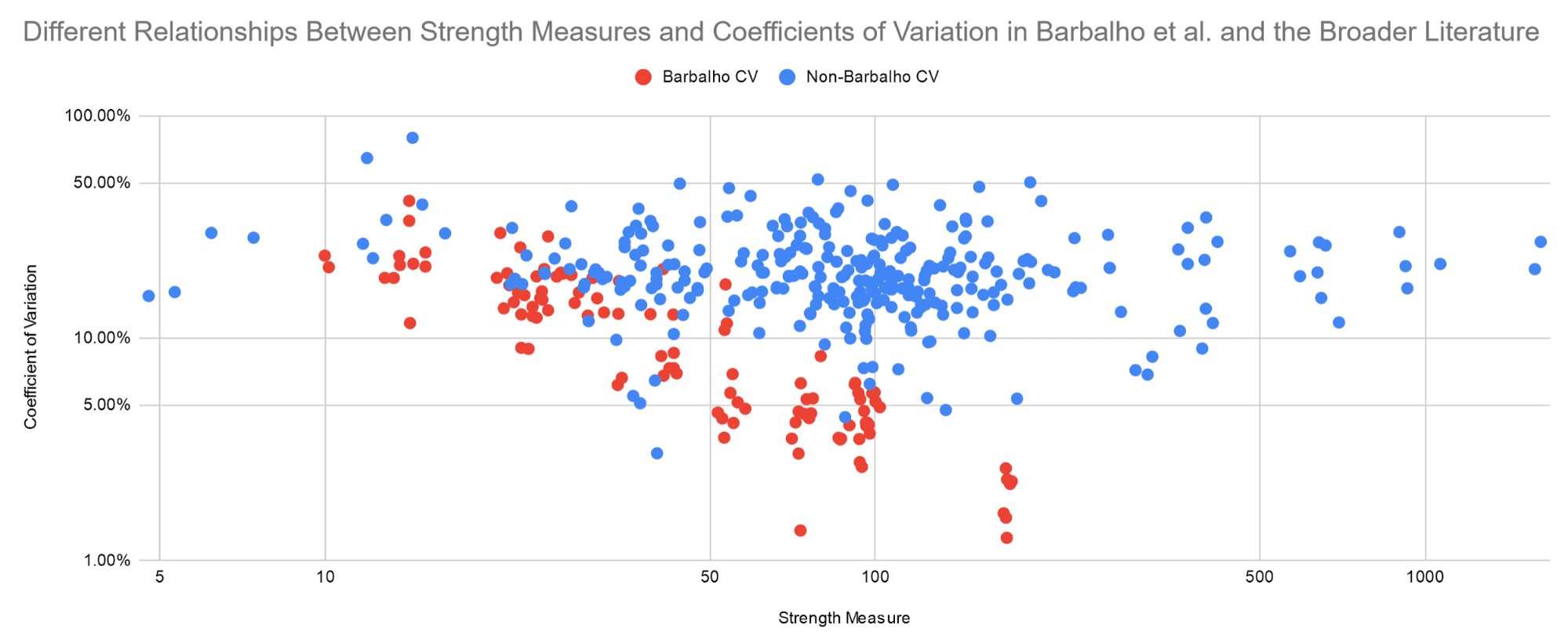
Let’s compare those two patterns in the broader literature – standard deviations scaling linearly with mean strength, and coefficients of variation being unaffected by mean strength – with the patterns seen in Barbalho’s research.
As you can see, in Barbalho’s research, mean strength and standard deviations are completely unrelated. From subjects curling 15kg to subjects leg pressing 175kg, standard deviations are generally somewhere between 2kg and 6kg, with an average just below 4kg. As a result, coefficients of variation decrease exponentially as a function of mean strength (R = -0.82).
On the following graphs, you can see these different trends plotted alongside each other. Note that both axes are log-scaled on both graphs.
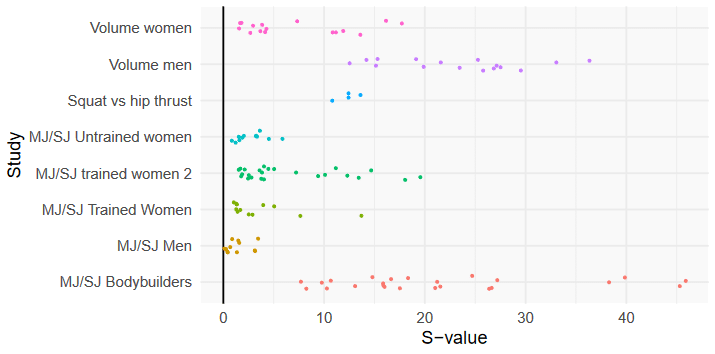
Additionally, the average coefficient of variation is way lower in Barbalho’s research than in the rest of the literature: 11.4 ± 8.0% vs. 20.9 ± 9.2% (S = 72.9; in other words, as surprising as flipping a coin and having it land “heads” 73 times in a row, if one assumes that the coefficients of variation should be similar).
Andrew performed a meta-regression (a statistical technique used to compare study results, while accounting for differences between studies) to see how unlikely it would be for the combinations of means and standard deviations observed in Barbalho’s studies to occur by chance, assuming that the relationships between those two variables should be similar. Here are the results:
All of the studies except for the multi-joint/single-joint training study on untrained women and the multi-joint/single-joint training study on untrained men have at least one S-value greater than 10, meaning most of these studies have some very unlikely pairs of means and standard deviations.
In Barbalho and Gentil’s defense, they’ve claimed that in many of these studies, Barbalho specifically screened for subjects who were all very similar at baseline. The papers don’t mention that recruitment criterion, but specifically recruiting homogeneous subjects could partially explain the tight standard deviations and low coefficients of variation. However, this potential explanation also has issues, which will be explained later.
Effect Sizes
To understand this section, there’s one more statistical concept you need to understand: effect sizes. While an S-value tells you how unlikely or surprising it would be for something to occur by chance (given the assumptions of your statistical model, etc., etc.), an effect size tells you how large a difference or a change is. There are lots of different types of effect sizes, but the most intuitive standardized effect size is probably Cohen’s D. A Cohen’s D effect size is almost like the inverse of a coefficient of variation. A coefficient of variation tells you how variable something is relative to its mean, while Cohen’s D tells you how large a mean is relative to a measure of variability. You calculate it by dividing a mean (generally a mean change in a measure, or a mean difference between groups) by a reference standard deviation (generally the standard deviation of a baseline measurement, or the pooled standard deviation of a baseline measurement over multiple groups).
So, for example, if a group of people currently benches 100 ± 5kg, they train for three months, and they put an average 10kg on their bench press, the Cohen’s D effect size would be 10/5 = 2. That tells you the mean change was twice as large as the standard deviation; in other words, the subjects improved their bench presses by two full standard deviations relative to their baseline, which is a whole lot of progress. If they put 10kg on their bench press, but the group mean and standard deviation were 100 ± 10kg to start with, the effect size would be 10/10 = 1. In other words, the lifters improved by one standard deviation, on average.
The traditional way to interpret a Cohen’s D effect size is that an effect size smaller than 0.20 is considered trivial, an effect size from 0.2-0.49 is considered small, an effect size from 0.5-0.79 is considered medium, and an effect size of 0.8 or greater is considered large. You can think about effect sizes in terms of percentiles. If someone started in the 50th percentile of the distribution, and improved their performance by an effect size of 0.2, they’d wind up in the 58th percentile – a small but possibly meaningful improvement. If someone started in the 50th percentile and improved their performance by an effect size of 0.8, they’d wind up in the 79th percentile – a pretty large improvement (going from middle of the pack, to just outside the top 20% of performers).
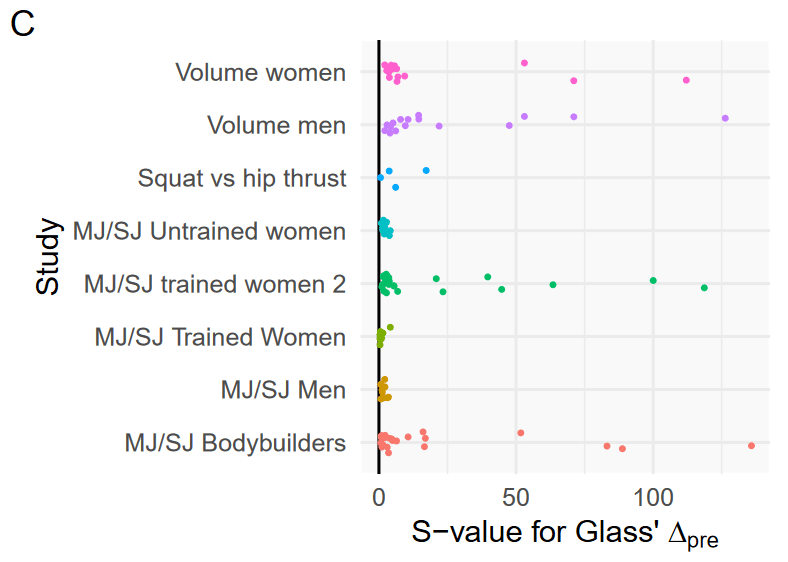
In the literature outside of Barbalho’s studies, the mean effect size for changes in strength is 1.21 ± 1.03. That tells you that the typical strength gains in most studies are pretty large (1.21 would be considered a large effect size), and that the variability between studies is pretty large (since the standard deviation is nearly as large as the mean). For Barbalho’s studies, the mean effect size for changes in strength is 3.79 ± 3.47. The tells you that the effect sizes in Barbalho’s studies also have quite a bit of variability (the standard deviation is almost as large as the mean), but the mean effect size itself is absolutely enormous – more than three times larger than the effect sizes in the rest of the literature. The difference is about as surprising as flipping a coin and having it land “heads” 42 times in a row (S = 41.7). Barbalho’s research also has a near-monopoly on enormous effect sizes. Within all 77 of the studies being analyzed (including Barbalho’s), there were 13 effect sizes larger than 10, and 41 effect sizes larger than 5. Barbalho’s studies accounted for 12 of the 13 effect sizes larger than 10, and 30 of the 41 effect sizes larger than 5. Within the rest of the literature, effect sizes larger than 5 occurred 3.7% of the time; in Barbalho’s studies, they occurred 26.8% of the time. In a meta-regression, some of the individual results had S-values of 100+.
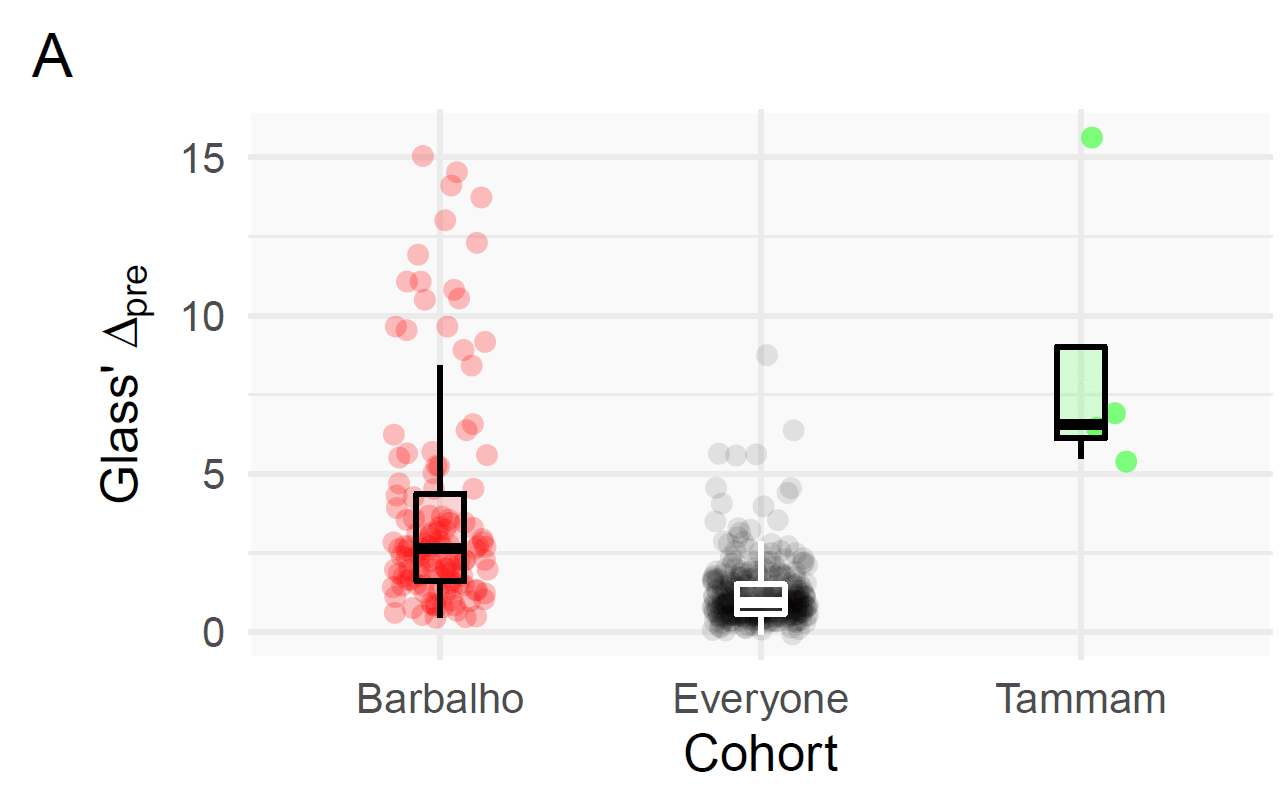
However, interestingly, percentage changes are similar in Barbalho’s research compared to the rest of the literature. Subjects in the rest of the literature got 24.0 ± 21.9% stronger, while subjects in Barbalho’s studies got 30.4 ± 28.4% stronger, on average. That’s not a particularly large difference, and it’s not nearly as surprising as the other differences we’ve seen so far (S = 5.3).
So, what explains the difference between the results we see when comparing effect sizes versus comparing percentage increases? After all, effect sizes and percent changes should both tell you about the magnitude of the change.
As it turns out, effect sizes and percentage changes are strongly associated in the rest of the literature. Here you can see the relationship between percentage changes in strength (x-axis) and effect sizes (y-axis).
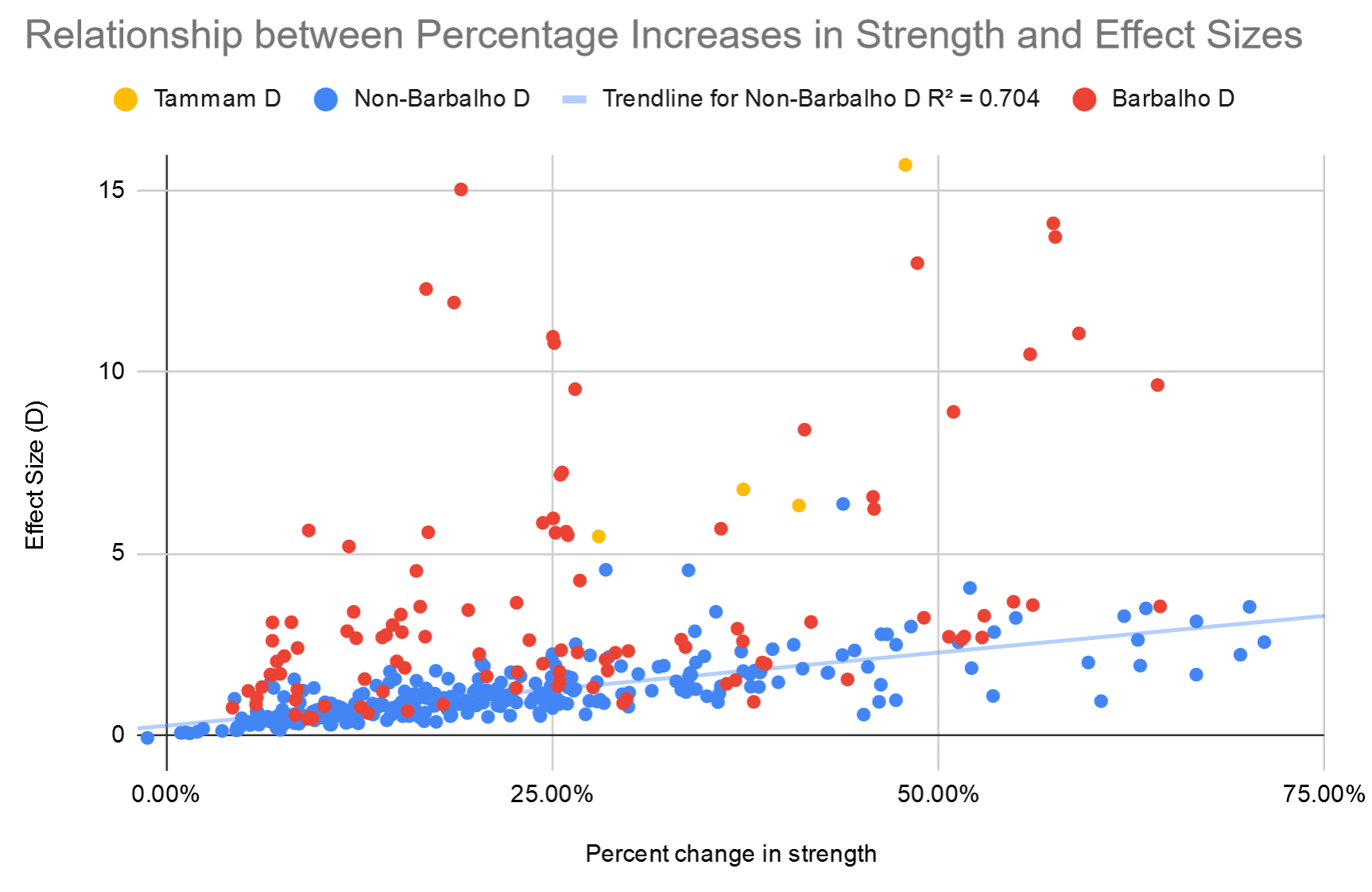
The one yellow study is a bit of an outlier, and was practically the only other study with Barbalho-esque effect sizes. It also had incredibly small standard deviations and coefficients of variation, much like Barbalho’s research (for example, unilateral leg press strength was 40.09 ± 1.22kg for one group, which implies that all subjects had leg press maxes that fell within the implausibly tight range of 38-42kg). With that study included, there’s a reasonably strong correlation between effect sizes and percent changes in strength (r = 0.68). With that study excluded as an outlier, there’s a very strong correlation between effect sizes and percent changes in strength (r = 0.84).
As you can see, many of the combinations of effect sizes and percent increases in strength in Barbalho’s studies live in their own little universe on the top left corner of the chart. Now, this isn’t a completely independent critique – since effect sizes are calculated in reference to pre-training standard deviations, and since Barbalho’s studies are characterized by having small standard deviations, effect sizes are almost guaranteed to be large – but it demonstrates the divergence between Barbalho’s research and the rest of the literature through another lens.
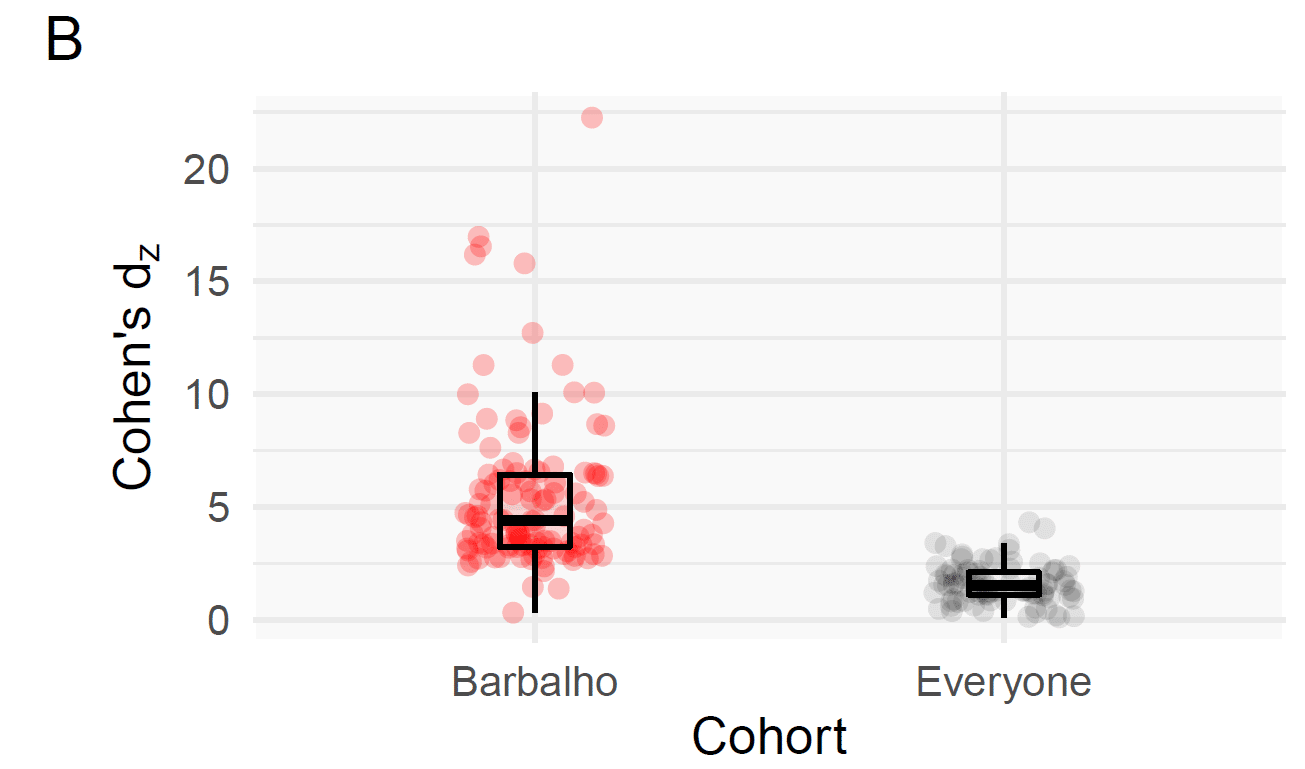
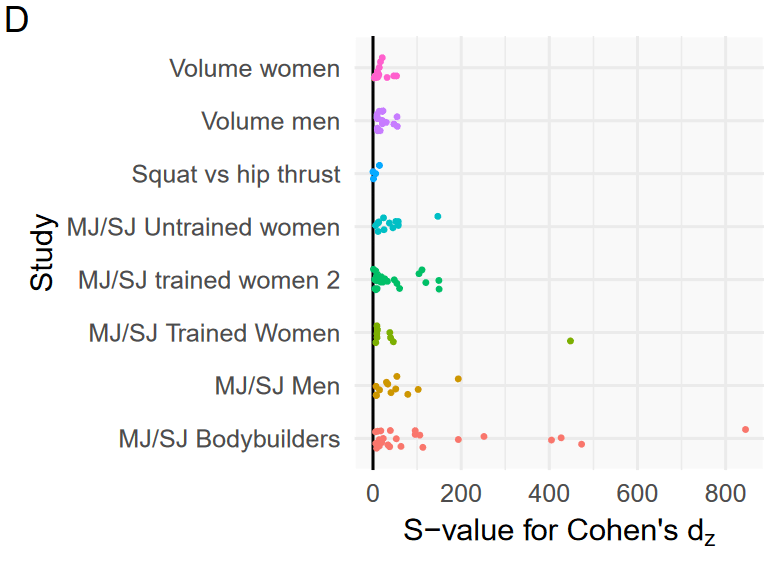
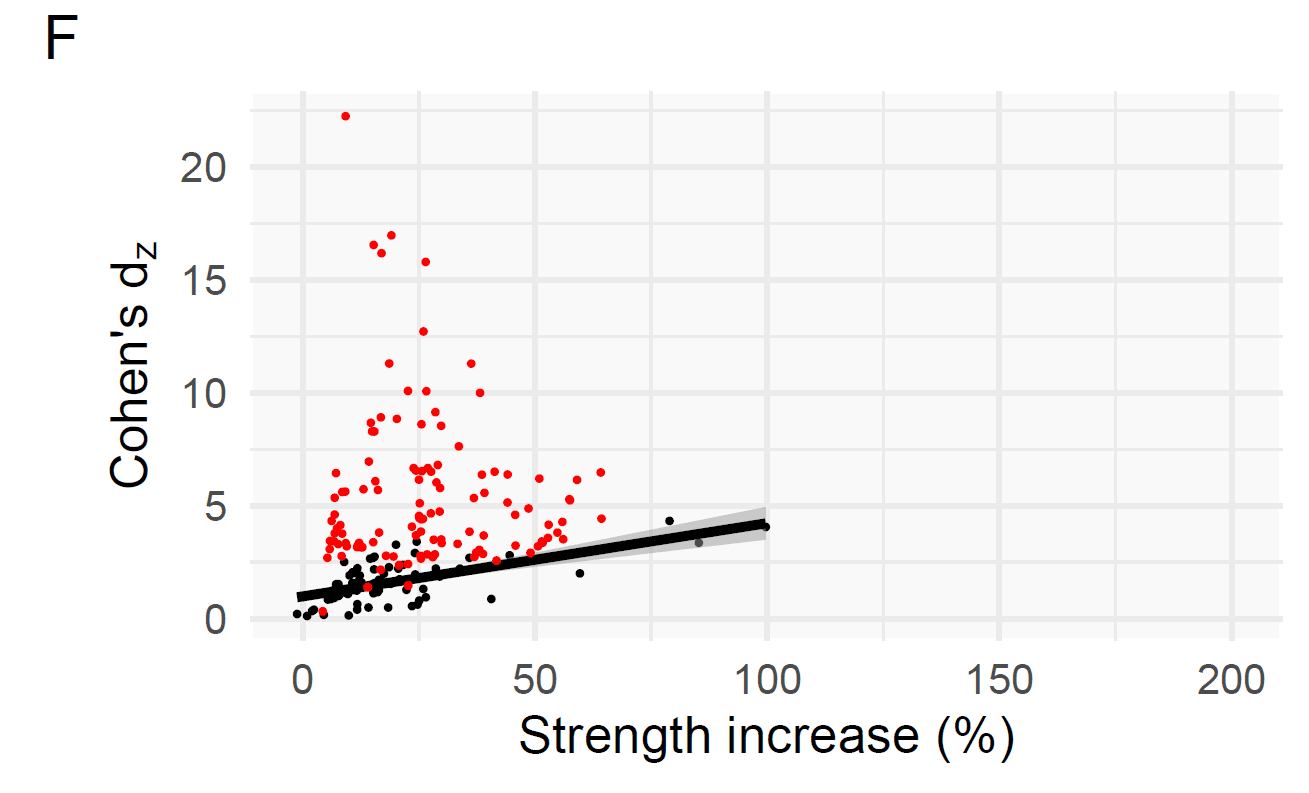
A different effect size metric is Cohen’s Dz. The difference between Cohen’s D and Cohen’s Dz is that you divide the average change by the pre-training standard deviation to calculate D values, whereas you divide the average change by the standard deviation of the change to calculate Dz values. In other words, instead of telling you the magnitude of the change relative to the baseline variability, it tells you the magnitude of the change relative to the variability of the change. As such, it’s sometimes referred to as a signal-to-noise ratio.
As one would expect, within the broader literature, as larger strength gains occur, Cohen’s Dz values increase (r = 0.64). However, within Barbalho’s research, there’s virtually no relationship between Dz values and the magnitude of strength gains. Furthermore, Barbalho’s reported Dz values are substantially larger than the Dz values reported in the rest of the literature (5.42 ± 3.46, versus 1.60 ± 0.85; S = 69.8). Andrew performed another meta-regression on Cohen’s Dz values, comparing individual results from Barbalho et al. to the Cohen’s Dz values observed in the rest of the literature. Multiple S-values in the 100s were observed, with a peak of 845. It should be noted that three strength changes in one of Barbalho’s studies actually have incalculable Dz values, because every subject had identical strength increases, so they couldn’t be included in this analysis.
Red dots represent Dz values from Barbalho’s studies, while black values represent Dz values from other studies. Of note, only 23 out of the 68 non-Barbalho studies in our database contained the information necessary for calculating Dz values.
Similarities in Effects Between Groups and Studies
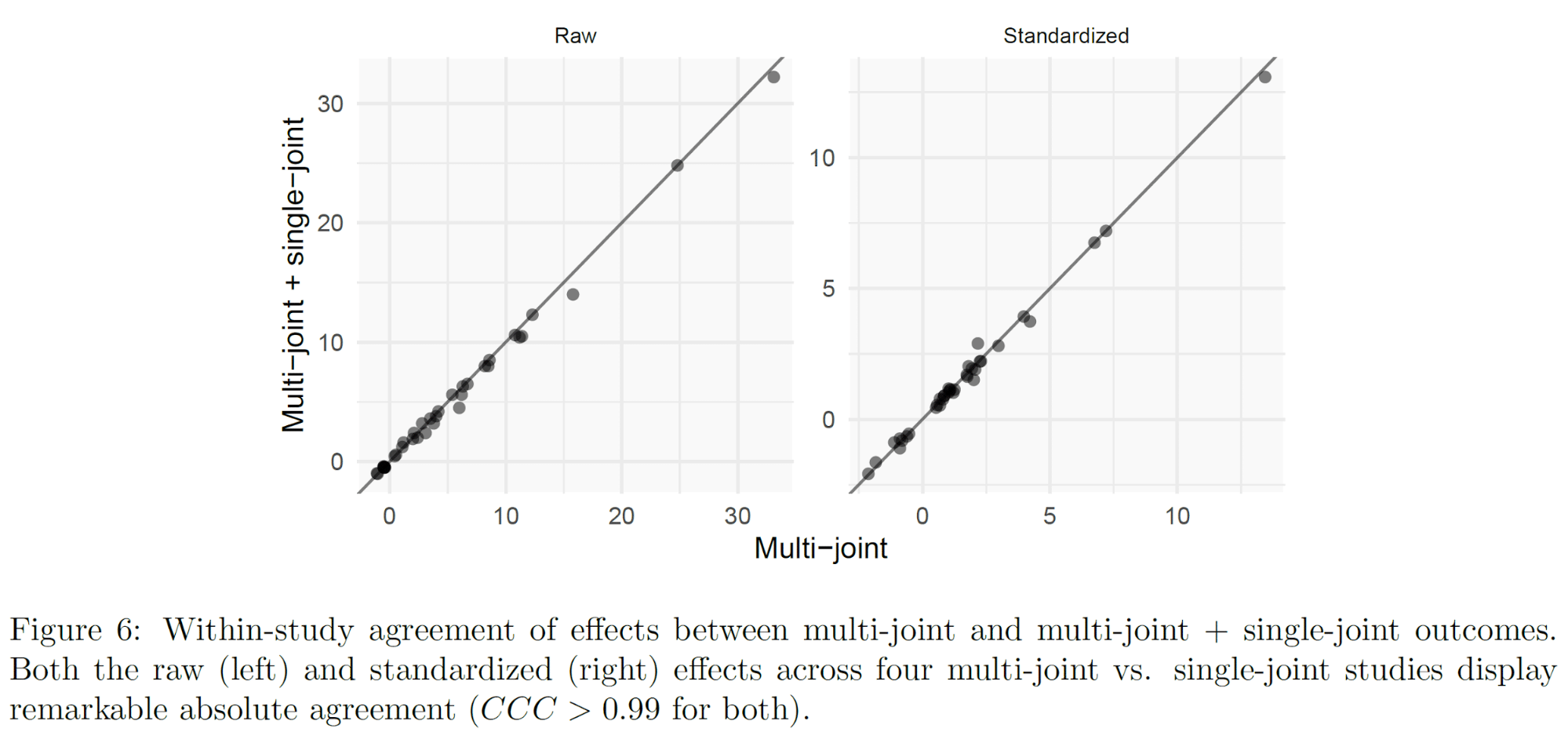
In Barbalho’s multi-joint vs. single-joint training studies (one, two, three, four), the multi-joint group and the multi-joint plus single-joint group generally have similar results across all measures. If one assumes that there is truly no benefit of adding single-joint exercises to a training program that already contains multi-joint exercises that target the same muscles, that wouldn’t initially seem like a very surprising finding. However, what is surprising is the strength of the association.
In the figures below, the effects in multi-joint training groups are on the x-axis, and the effects in multi-joint plus single-joint training groups are on the y-axis. For example, if the subjects in the multi-joint group put 10kg on their bench press in one study, and the subjects in the multi-joint plus single-joint group put 11kg on their bench in the same study, that point would be plotted (x = 10, y = 11). Raw effects (on the left) are measures like strength gains in kilograms. Standardized effects (on the right) are effect sizes. As you can see, these effects are almost perfectly correlated. The concordance correlation coefficient is Rc>0.99; this means that not only are corresponding effects correlated with each other; they also fall almost perfectly along the line of identity (x = y).
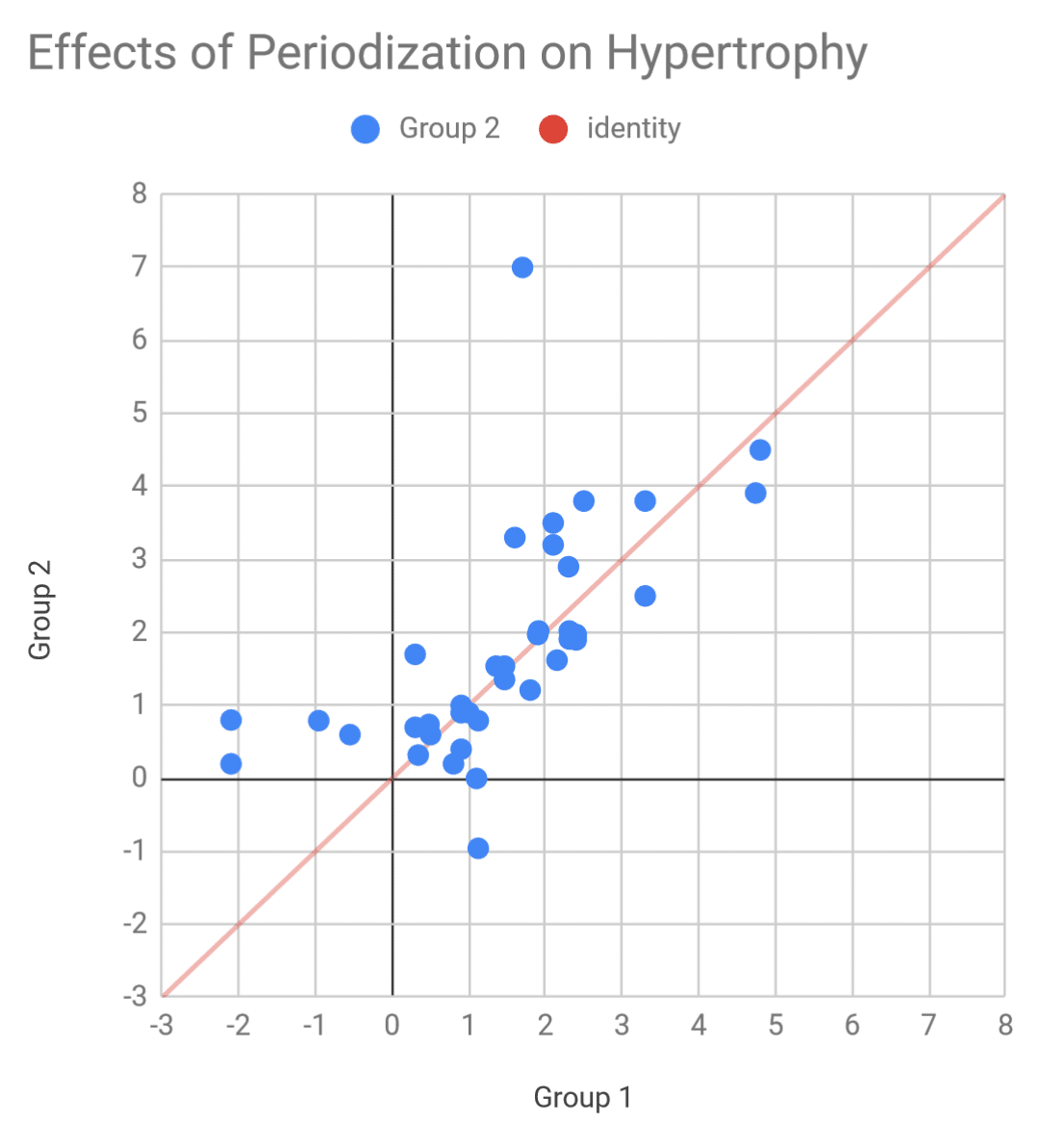
As a point of contrast, we also know that periodized and non-periodized training tend to have similar effects on muscle growth, and that periodization style doesn’t seem to significantly influence muscle growth. If we chart the hypertrophy effects in the periodization literature in a similar fashion, you can see that there’s still considerably more heterogeneity, and the data points don’t all fall as nicely along the line of identity. The concordance correlation coefficient is thus substantially lower (Rc=0.61).
It’s hard to statistically describe just how unlikely it is for the effects in Barbalho’s multi-joint vs. single-joint papers to be so tightly correlated, but this comparison to the periodization literature suggests that the effects in Barbalho’s multi-joint vs. single-joint papers are far more tightly correlated than would be expected.
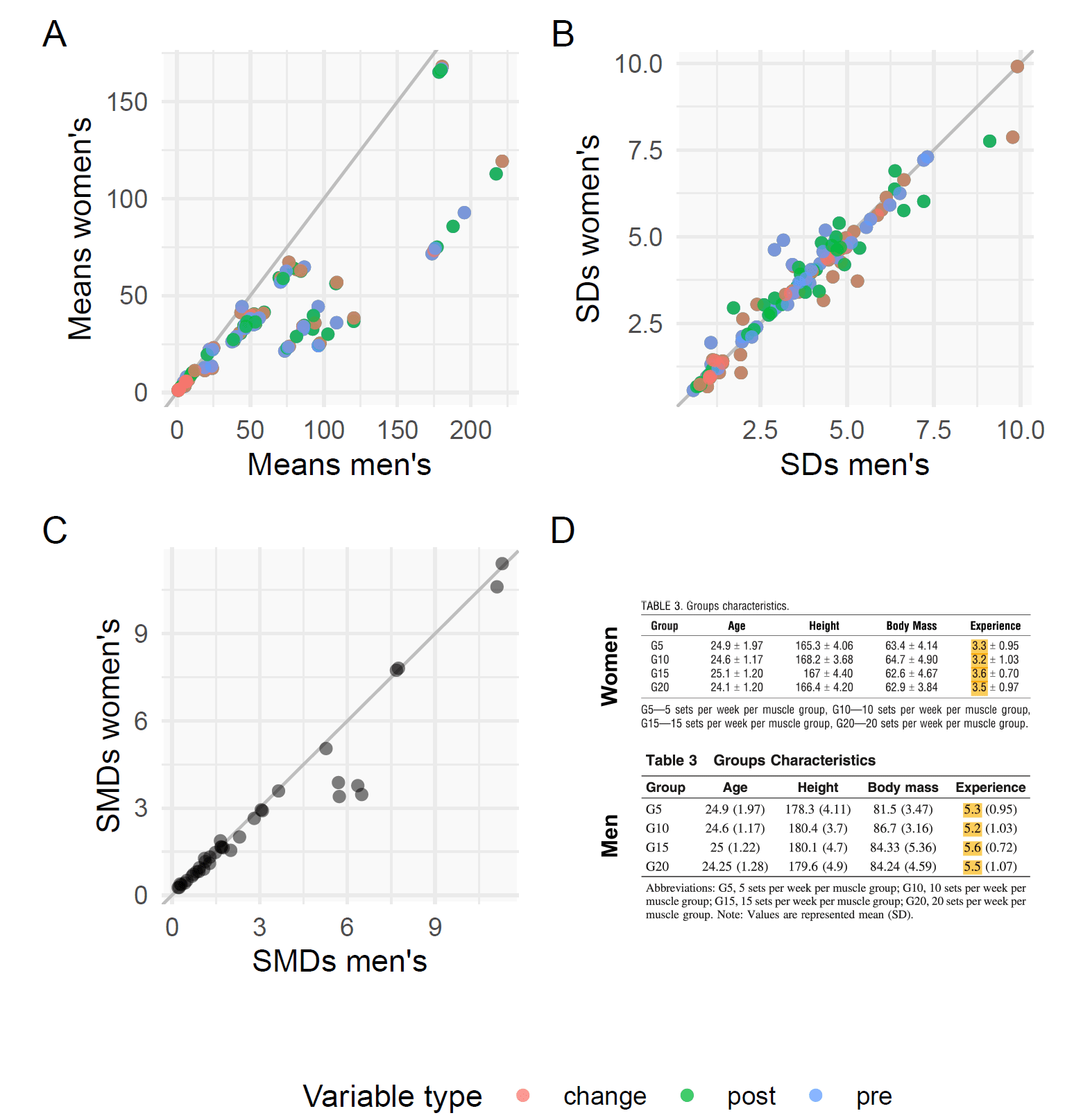
A similar relationship was found in Barbalho’s two volume studies. Both studies examined the effects of 5, 10, 15, or 20 sets per muscle group per week on muscle growth and strength gains; one study was carried out with female subjects, and the other study was carried out with male subjects. Corresponding measurements and standard deviations were mostly tightly correlated in these two studies as well. In several instances, the raw means were smaller in the female study, but the data appear as they would if the data points were simply shifted down off the line of identity. One clear example is shown in the figure below – in all four groups, the female subjects had exactly two fewer years of training experience than the male subjects. Similar relationships existed for other variables. For example, all four groups of males squatted either 71.9, 72.0, or 72.1kg more than each corresponding group of females (96.2, 96.8, 97.3, 96.3 vs. 24.2, 24.8, 25.4, 24.2).
Fat Loss in Elderly Subjects
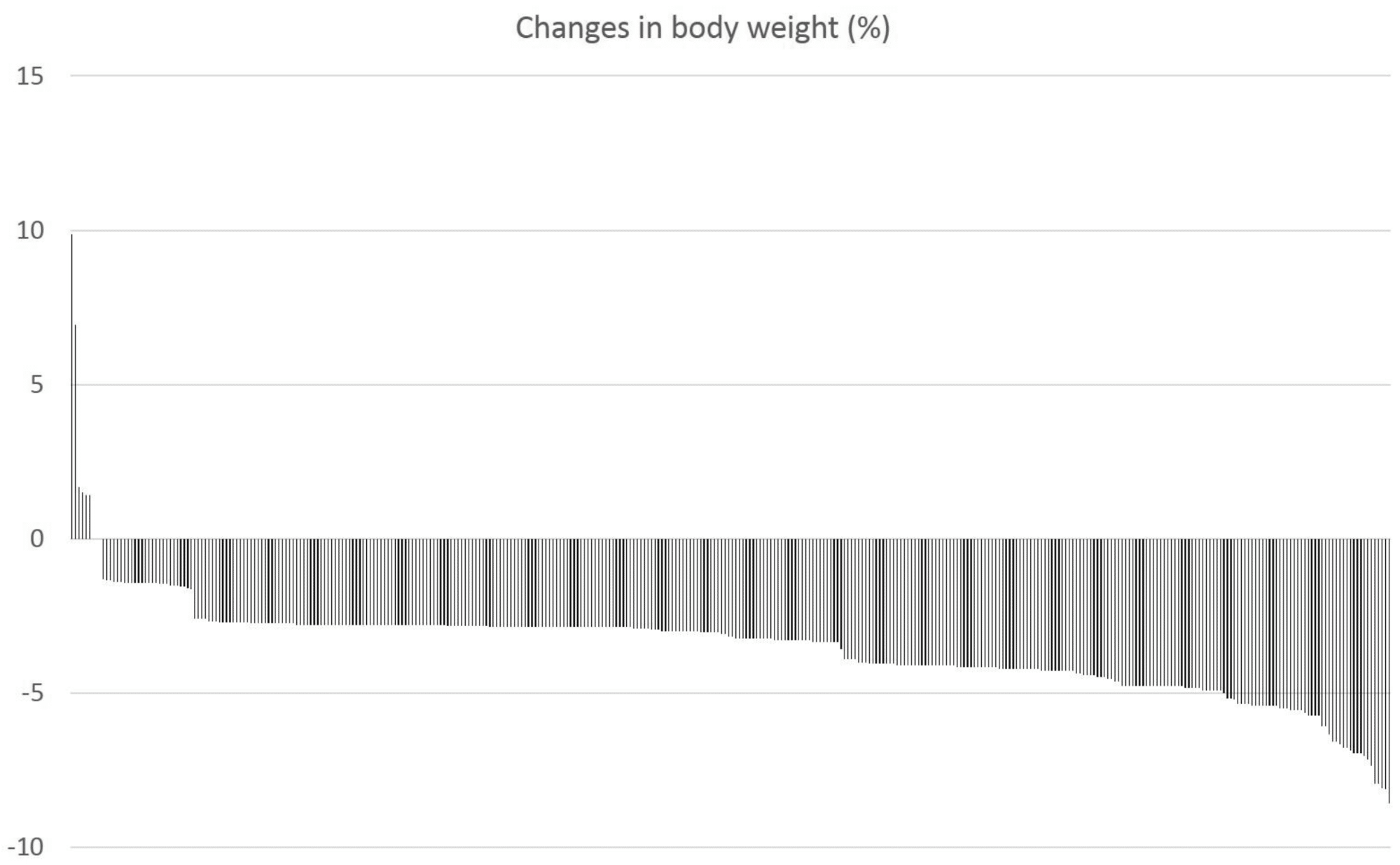
Let’s turn our attention to the volume study carried out on elderly women. In this study, 400+ women, mostly in their late 60s or early 70s, carried out a resistance training program for 12 weeks. They were specifically instructed to not change their dietary habits, but nutrition wasn’t controlled. 376 subjects completed the study. Of those 376 subjects, 370 lost weight (98.4%).
We’ve not seen any other large resistance training studies (without a diet component) in elderly subjects report weight loss in such a large proportion of subjects. As a point of comparison, Ahtiainen et al reported that 132 out of 285 subjects (46.3%) lost weight in a similar study, which is more-or-less typical for resistance training studies without dietary controls. Those proportions are drastically different (S = 56.0). Discussions with Dr. Gentil and Experimental Gerontology about this study are ongoing.
Unlikely Trends in Raw Data
Up to this point, all of the findings I’ve discussed are things anyone could have noticed if they were willing to spend a little time digging into these studies, organizing their results, and comparing them to other research in the field. These were the sorts of anomalies that convinced James Steele to join our group and share some of the raw data with us. And once we were able to dig into the raw data, we discovered even more anomalous data patterns.
Volume Studies, Part Two
When you open up a datasheet, one of the first things you can do to start exploring the relationships between variables is to construct a correlation matrix. A correlation matrix is just a big table that shows you the strength of the associations between each pair of variables in the datasheet. It’s convenient to color-code correlation matrices so that your eye can immediately be drawn to strong correlations, instead of needing to sort through each cell of the spreadsheet one by one.
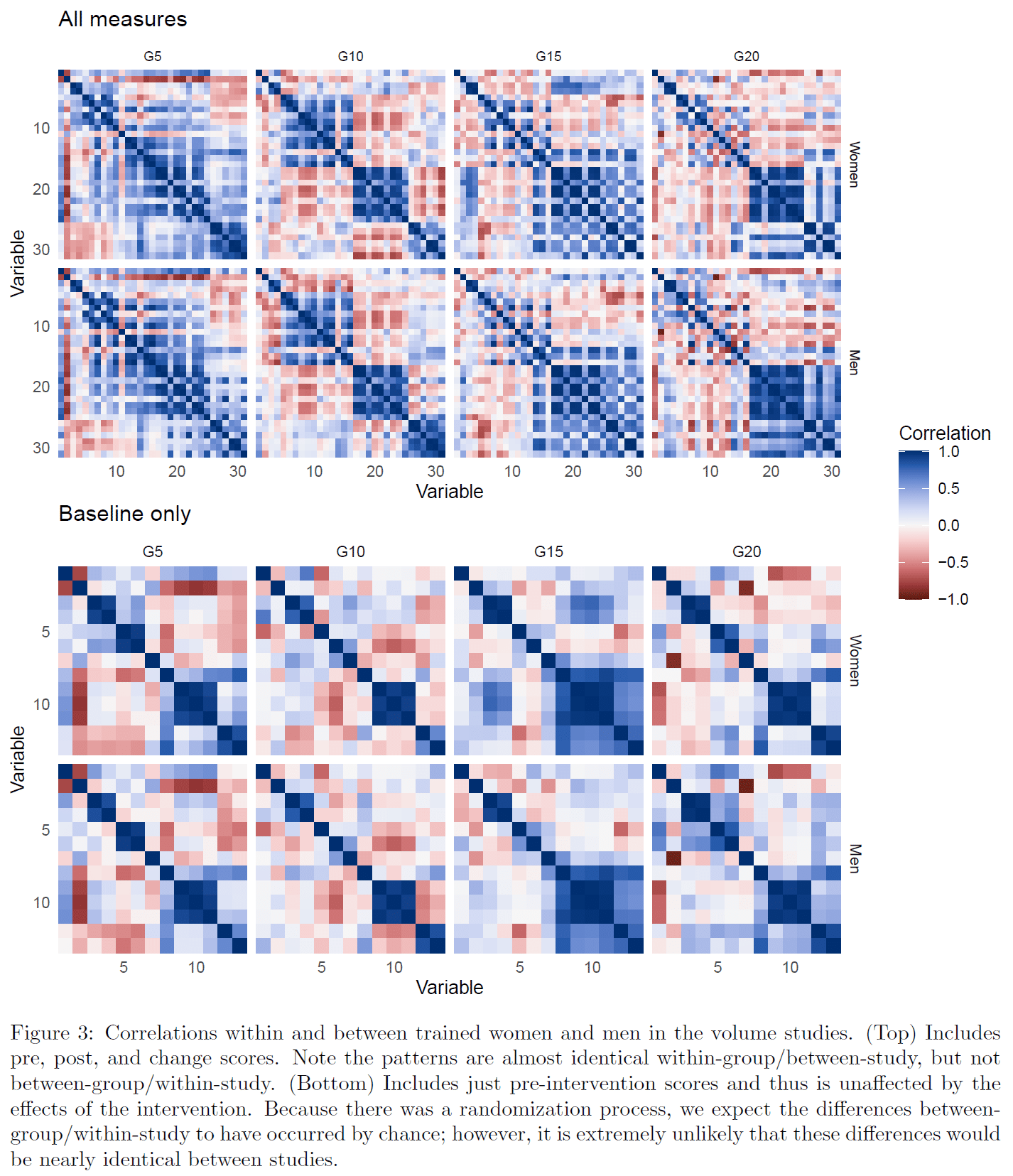
Andrew created color-coded correlation matrices for each of the groups in the male and female volume studies, and noticed that the set of correlation matrices in the female study looked incredibly similar to the set of correlation matrices in the male study: the correlation matrix for the 5-set group in the female study looked very similar to the correlation matrix for the 5-set group in the male study, the correlation matrix for the 10-set group in the female study looked very similar to the correlation matrix for the 10-set group in the male study, and so on. However, the correlation matrix for the 5-set group in each study looked considerably different from the correlation matrix for the 10-, 15-, and 20-set groups in the same study.
That’s not the type of relationship one would expect under assumptions of randomization.
First off, it’s unexpected for correlation matrices to look similar when all variables are included. Some variables should have predictable correlations (e.g. height should be positively correlated with weight, bench press strength should be positively correlated with triceps extension strength, etc.). However, other correlations should be essentially random (e.g. there’s no reason to expect chronological age to be associated with height when all of your subjects are adults; you may have a weak correlation, or you may wind up with a modest positive or negative correlation due purely to chance). When you’re color-coding a pair of correlation matrices, and a lot of the correlations should be essentially random, you should expect those correlation matrices to look considerably different. Moreover, in both of these studies, the 5-set and 10-set groups got virtually identical results across all outcome measures, so if pairs of correlation matrices were to look similar, you’d expect to see that similarity when comparing the 5-set and 10-set groups within each study.
Instead, here’s how the correlation matrices look.
So, that’s clearly not what one would expect. But how atypical is it? As a first point of comparison, we compared the (deep breath) strength of the correlation between the corresponding correlation coefficients between studies (e.g. 5-set female group vs. 5-set male group), with the strength of the correlation between the corresponding correlation coefficients between groups within each study. When comparing between studies (5-set females vs. 5-set males, 10-set females vs. 10-set males, etc.), the correlation was always strong (R > 0.8). When comparing between groups within each study, the correlation was always weak. For example, the comparison between the 5-set and 10-set groups within each study yielded R = 0.26 for the female study and R = 0.35 for the male study.
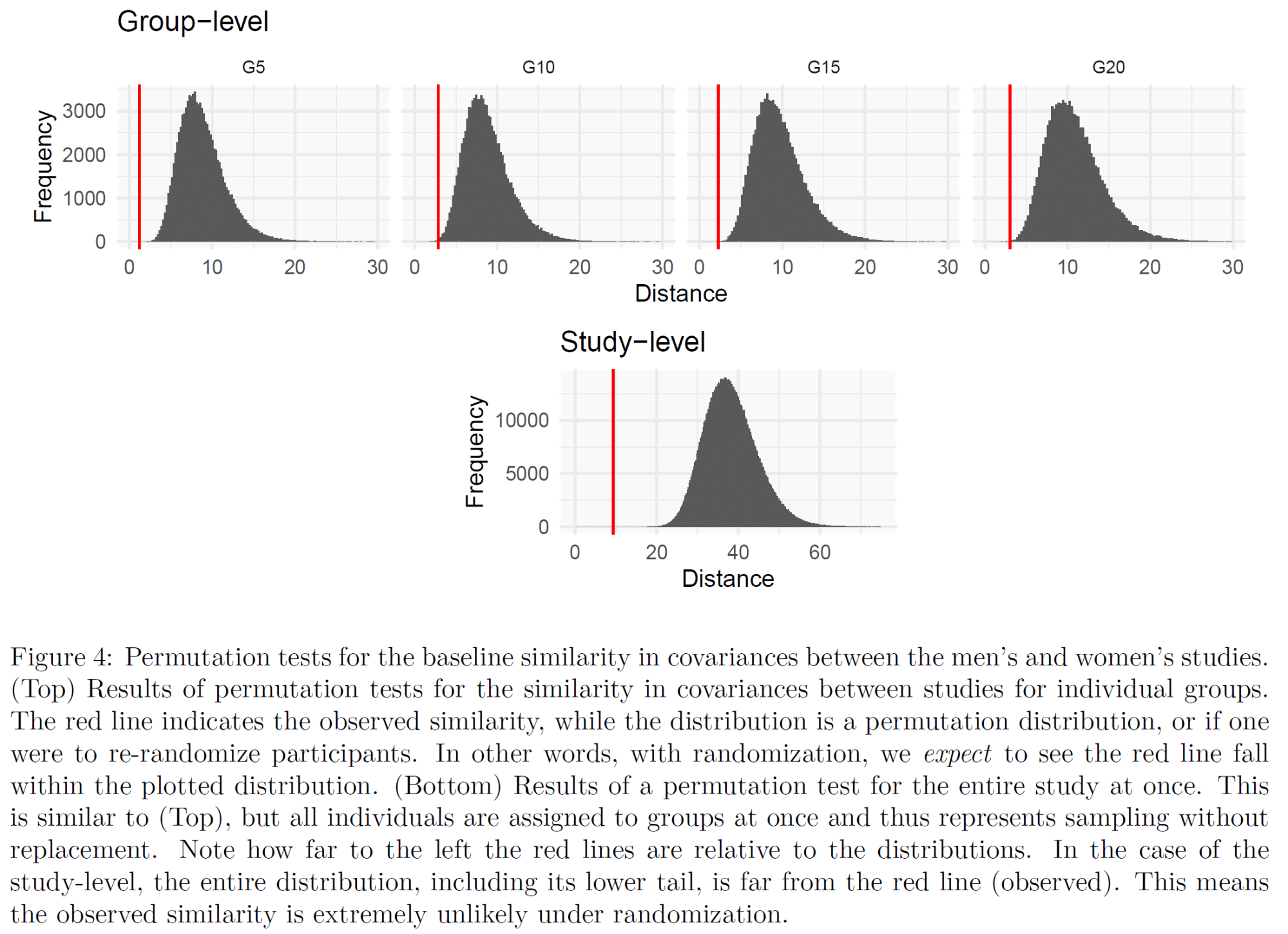
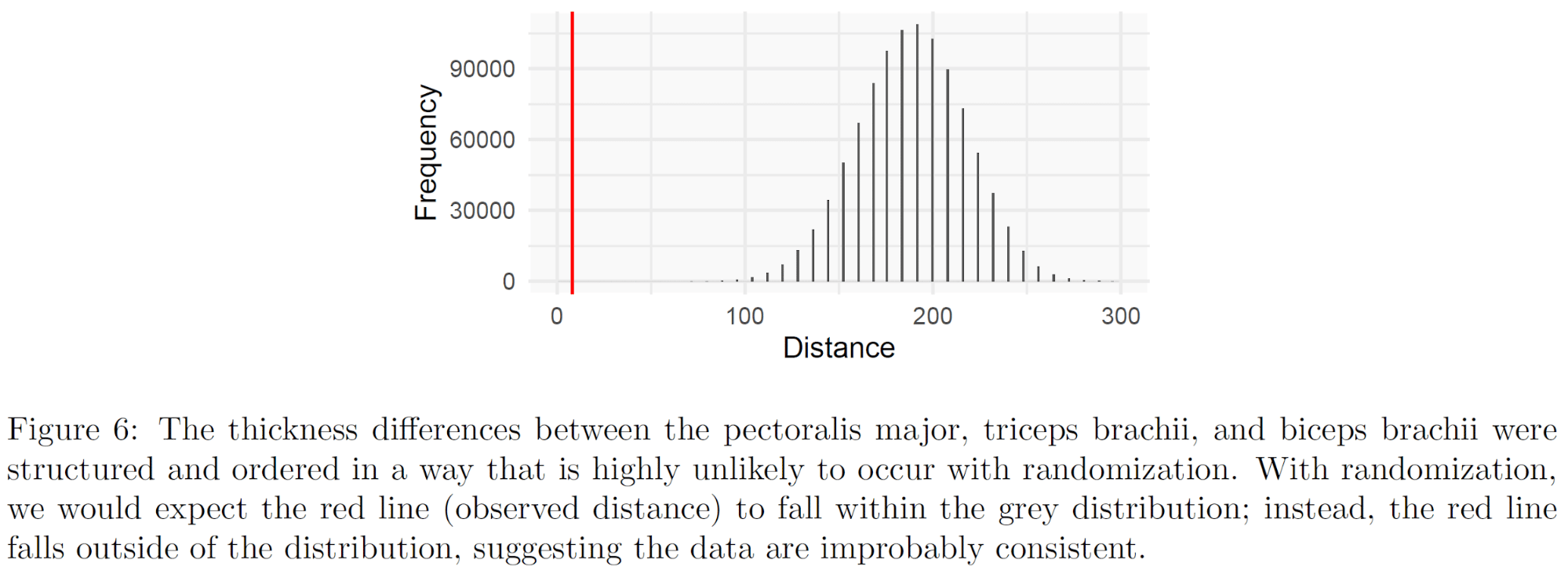
So, how unlikely is it for us to see a pattern like this due to chance? Since the subjects were randomly assigned to groups, we can strip away any variables that were impacted by the intervention (e.g. changes in strength and muscle size, and post-training strength and muscle thickness measures), re-randomize the subjects, see what sorts of patterns emerge, and then see how extreme the observed patterns are compared to the average patterns you’d anticipate with randomization. For each group independently, it’s very unlikely to see such a pattern by chance (S = 10.7-16.6+). And on a study level, to see such a pattern across all four pairs of corresponding groups is even less likely. Andrew ran 1,000,000 simulations, re-randomizing the subjects, and none of the simulations came particularly close to producing correlations between corresponding groups in each study as strong as were observed in Barbalho’s two volume studies (S > 19.9).
Dr. Gentil has claimed that both of these studies were carried out as described in their respective papers, but that an undergraduate student responsible for transcribing the data in the male volume study “made much of the data” because he was “too busy to do the job.” Thus, the male volume study was retracted.
More Data Anomalies in the Female Volume Study
The female volume study contains two additional data anomalies that are completely unrelated to the similarities between the male and female volume studies.
In the datasheet for the female volume study (and, for that matter, in every study by Barbalho et al for which we have the raw data), there are considerably more even numbers than odd numbers. Virtually all of the strength measurements are even, which suggests that the researchers mostly increase loads in increments of 2kg when testing strength. However, even when disregarding strength measurements, there are nearly twice as many even numbers in the datasheet, even for measurements that should have a roughly 50/50 distribution of even and odd numbers (like age, height, or muscle thickness measurements). This distribution of even and odd numbers in the female volume study would be very unlikely to occur by chance (S = 52.0 with strength measures included, and S = 25.8 with strength measures excluded).
Another quirk in the female volume study is that the baseline measures of upper body muscle thickness follow an unexpectedly predictable pattern in the 5-set and 15-set groups, and the 10-set and 20-set groups. If, for the first subject in the 5-set group, the triceps were 10mm thicker than the biceps, the triceps would also be 10mm thicker than the biceps for the first subject in the 15-set group. If the triceps were 2mm thicker than the pecs for the fourth subject in the 10-set groups, the triceps would also be 2mm thicker than the pecs for the fourth subject in the 20-set group. This pattern held for all comparisons of biceps, triceps, and pec thickness between both pairs of groups, with just one exception (so it held in 59 out of 60 possible comparisons).
Since the subjects were randomly assigned to groups, and since this pattern was observed for baseline measures (i.e. measures that were unaffected by group assignment) we were (Andrew was) able to re-randomize the subjects 1,000,000 times to see how unlikely this pattern was. Turns out, it was highly unlikely: S = 32.3.
Ordered Flexed Arm Circumferences
In two of Barbalho’s studies (one, two) that assessed flexed arm circumference, the data in both groups consisted of just two numbers, with a “run” of the first number followed by a “run” of the second number. In all four cases (two groups per study), the “runs” were arranged low-to-high. Here’s what I mean: the flexed arm circumference data were, in order, 0.8, 0.8, 0.8, 0.8, 0.8, 1.1, 1.1, 1.1, 1.1, 1.1 for group 1 and 1, 1, 1, 1, 1, 1.4, 1.4, 1.4, 1.4, 1.4 for group 2 in the first study, and 0.3, 0.3, 0.3, 0.5, 0.5, 0.5, 0.5, 0.5 for group 1 and 0.4, 0.4, 0.4, 0.4, 0.5, 0.5, 0.5, 0.5, 0.5 for group 2 in the second study. To the best of our knowledge, the data had not been sorted to produce this pattern (if that occurred, the subjects were re-numbered after the fact).
So, that’s not what one would expect. How atypical is it? Within each study independently, if we already assume that it’s fine and normal for each column of data to consist of just two numbers, it’s pretty unlikely for those two numbers to exist as discrete “runs,” but not as unlikely as some of the other data anomalies we’ve explored so far: S = 15.9 for the first study, and S = 9.5 for the second study. It’s even less likely for this pattern to emerge in two different studies: S = 28.8. And it’s less likely yet for the “runs” to always be arranged low to high: S = 33.3.
And remember, we’re not even factoring in the likelihood of each group only having two different flexed arm circumference measures (i.e. all 0.8s or 1.1s, with no 0.9s or 1.0s mixed in). It’s a trend that’s as surprising as flipping “heads” 33 times in a row, even if we start with very charitable assumptions.
Identical Strength Increases
As previously mentioned, in one of Barbalho’s studies, all subjects experienced identical strength increases in three different measures. Elbow extension and elbow flexion strength changed by the exact same amount in all subjects in the multi-joint group, and pulldown strength changed by the exact same amount in all subjects in the multi-joint plus single-joint group. Thus, the Cohen’s Dz values are literally incalculable (the standard deviations for the change scores are 0, and you can’t divide by 0). None of us are aware of any other instances of such remarkably consistent strength gains elsewhere in the literature, much less three instances in one study.
Implausible Strength Gains
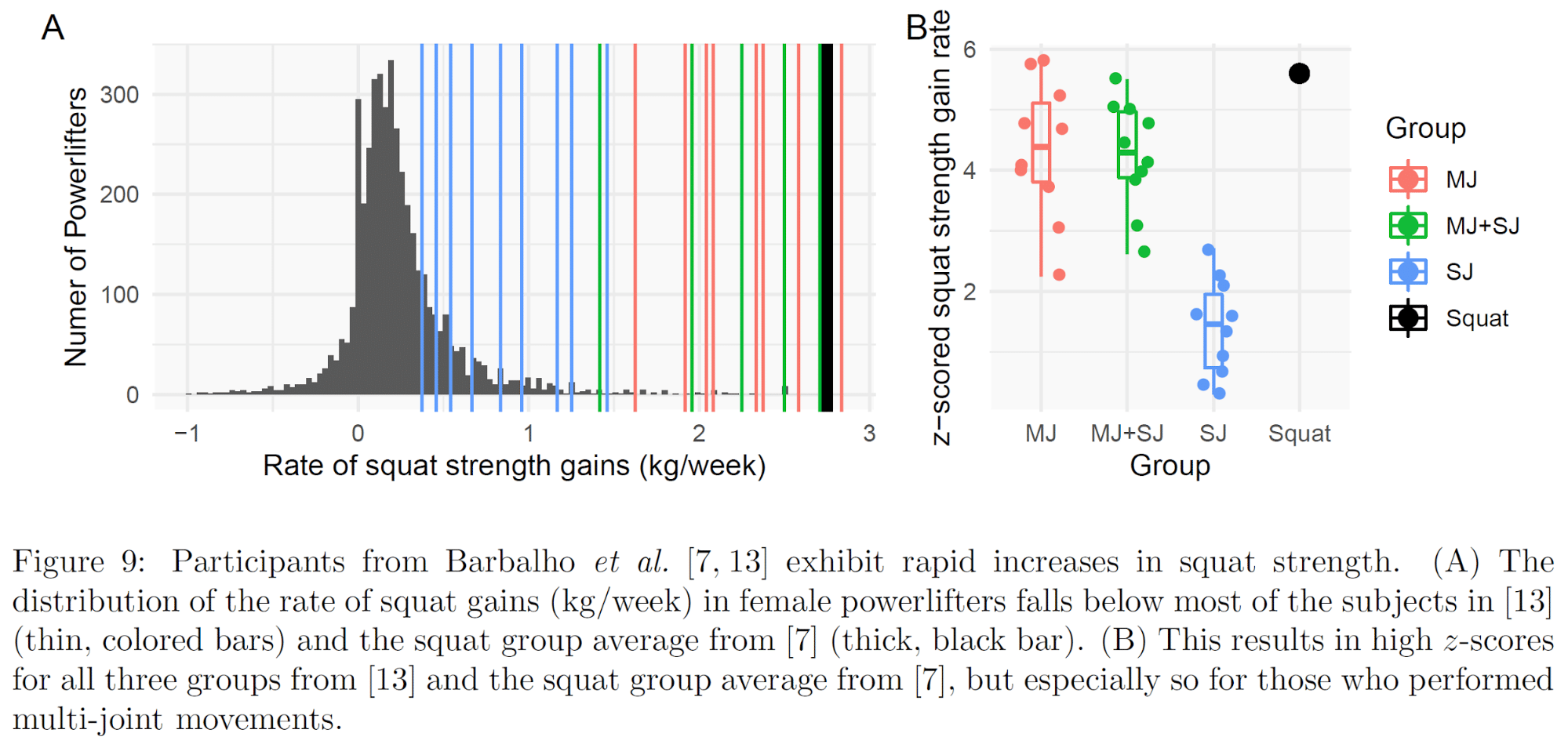
As mentioned in the intro, the strength gains in the squat group of Barbalho’s squat vs. hip thrust study were eye-popping: 33kg in just 12 weeks, which would have taken the lifters from 15th to the 65th percentile of their weight class if they competed in powerlifting. In a more recent study, over 6 months, two groups of female subjects who weighed approximately 63.3kg increased their squats from 91.8kg to 143.8kg, for an increase of 51kg. If they competed in the 63kg class in powerlifting, their squats would have improved from the 22nd percentile to the 94th percentile – modestly competitive to borderline world-class. In fact, there was one subject who would have broken the Brazilian national record in the squat if she would have completed her post-test on a powerlifting platform. She squatted 163kg at a body mass of 57kg (359lb at 125lb). The Brazilian record in the 57kg class is 160kg. In fact, she would have been just 15.5kg off Maria Htee’s world record of 178.5. Since she improved her squat by 68kg (95kg to 163kg) in a mere 6 months, at a rate of 2.83kg per squat workout, and a rate of almost 1kg per set of squats performed, she should be able to reel Maria in soon. The earlier squat vs. hip thrust study detailed how Barbalho’s subjects are required to perform full squats (to ~140 degrees of knee flexion; approximately 120 degrees of knee flexion generally coincides with legal depth for powerlifting), so judging shouldn’t be an issue for this budding squat prodigy either.
What’s even more striking is that the subjects who didn’t even train their squats for 6 months in Barbalho’s more recent study still improved their squat 1RMs by an average of 20.8kg (with a range of 9-35kg range) from 91.7 to 112.5kg. We filtered the OpenPowerlifting database down to female squatters of similar age and skill (allometrically scaled squat strength) to compare the rates of progress seen in competitive powerlifters vs. Barbalho’s subjects. Every single one of Barbalho’s subjects – including subjects who didn’t even train their squats for six months – gained squat strength faster than the median rate of progress observed in comparable female powerlifters.
Relationship Between Squat and Hip Thrust Strength
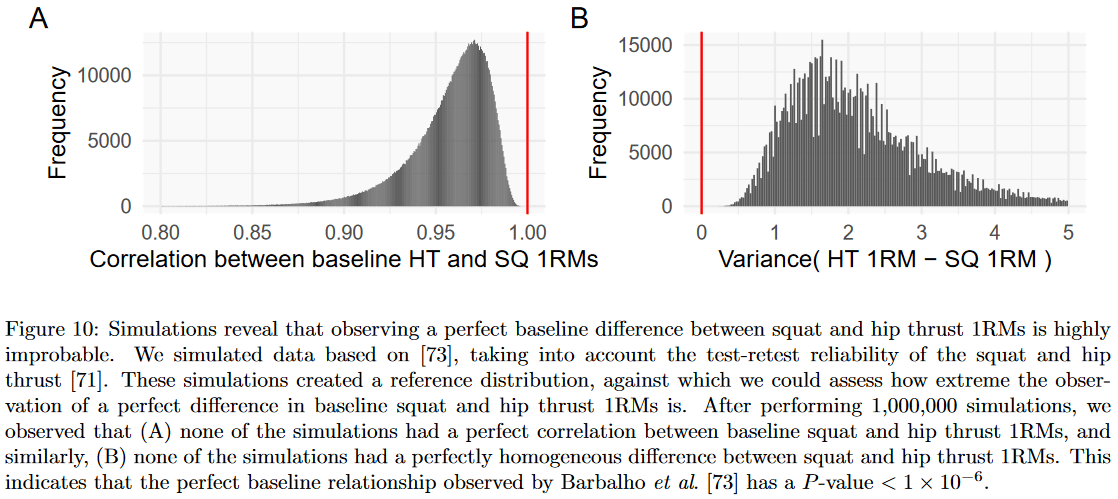
In the same study, every subject hip thrusted exactly 8kg more than they squatted. In other words, there was a perfect correlation between baseline squat and hip thrust strength (r = 1). We are unaware of any other instance in the literature where two strength measures are perfectly correlated.
Extreme Homogeneity
Callback time!
Near the start of this article, remember how I mentioned that many of the standard deviations in these studies were incredibly small (low coefficients of variation)? And remember how I said Barbalho and Gentil’s explanation for this oddity was that Barbalho specifically screened for subjects who were very similar at baseline?
That explanation hits a pretty major snag.
Enter the chain rule. The chain rule states that the probability of A and B occurring together is always lower than or equal to the probability of A occurring independently, regardless of B. For example, the proportion of the population that is both male AND has brown hair is smaller than the proportion of the population that is male. The proportion of the population that is male AND has brown hair AND is right-handed is smaller than the proportion of the population that is male AND has brown hair. It’s not uncommon to be male, or to have brown hair, or to be right-handed, but every time you add another condition, you whittle away another slice of the broader population, leaving you with a smaller and smaller proportion of your initial population.
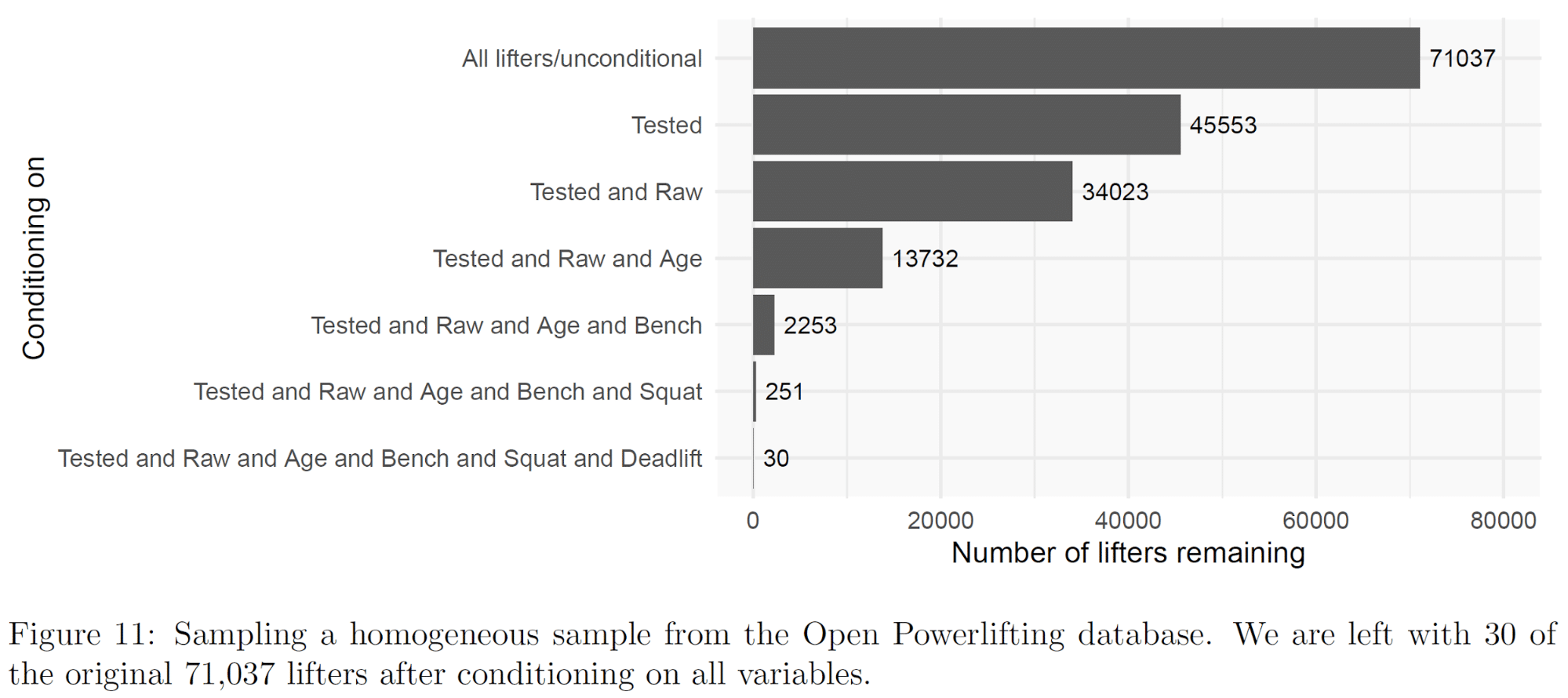
To illustrate the chain rule in action, we downloaded the Open Powerlifting dataset and got to work. We wanted to see if we could recruit a population of lifters who were similar across as many factors as Barbalho’s subjects. After downloading the dataset, we started by cleaning things up (removing lifters who bombed out or competed in single-lift events, and removing all but the most recent competition performance for each lifter). To keep things simple, we went with just male lifters. After cleaning up the dataset, we were left with data from 71,037 lifters.
First, we filtered the pool down to drug-tested lifters. That left us with about 45,000 lifters. Next, we filtered the pool down to raw AND drug-tested lifters. That left us with about 33,000 lifters. Next, we filtered the pool down to raw AND drug-tested AND open or junior-class lifters (ages 20-34). That left us with about 13,000 lifters. From there, we wanted to narrow things down to a population that was as homogeneous as the subjects in Barbalho’s studies (standard deviations of 5kg for each lift, to be charitable), that retained the same correlational structure as the initial population (since strength measures that “should” be correlated generally are still correlated in Barbalho’s studies). To do that, we looked for lifters who were close to the means (of the remaining population) for each lift. That left us with about 2,250 lifters when we just filtered people out who didn’t bench the correct amount. When we added squat and deadlift into the mix, we were left with just 30 lifters out of an initial population of approximately 71,000 powerlifters.
If we extrapolate this to Barbalho’s studies on trained subjects, that would mean that he’d need to be surrounded by a population of 70,000 males who engage in resistance training, and he’d need to test about 13,000 people (assuming people on drugs, people who fell outside the target age range, and people who only lifted equipped were automatically excluded) to recruit 30 subjects whose baseline data were sufficiently homogeneous.
Also keep in mind, assuming we can extrapolate from powerlifters to Barbalho’s target population is incredibly generous. Powerlifters test 1RM strength, which is prone to less variability than 10RM strength (which is what Barbalho tests in many of his studies). There are also pretty strong correlations between squat, bench press, and deadlift strength among powerlifters, since full-power competitors specifically train to maximize performance in all three lifts. There are almost certainly weaker correlations between, say, 10RM knee extension and 10RM lat pull-down in untrained populations, or among trained lifters who don’t train with a singular focus on maximizing 10RM knee extension and lat pull-down strength. With weaker correlations between lifts, you’d “lose” more potential subjects with each condition added under the chain rule. In our example, we were also more lenient with the age range we specified (20-34; the subjects in many of Barbalho’s studies seem to be between 20 and 26 years old). We also didn’t specify how much our powerlifters had to weigh, whereas Barbalho’s subjects generally fall within fairly tight weight ranges. We also had no way of specifying how many years of resistance training experience our powerlifters needed to have, whereas Barbalho’s trained lifters generally have a tight range of training experience (2-5 years, or 4-7 years). Since we knew the average bench, squat, and deadlift for our target population, we could specifically look for people who were close to those population averages, which increases the proportion of people who’d be able to fall within a tight range for three different lifts; since the population average 10RM knee extension and triceps extension (for example) would be unknown for Barbalho, he wouldn’t be able to be as precise in his screening, and he’d thus “lose” a larger percentage of potential subjects with each additional condition, based on how much his targeted sample means differed from the population means. Most importantly, we only filtered our population down until it had tight standard deviations across 3 lifts. Many of Barbalho’s studies test 5 or 6 lifts, and also have tight standard deviations for 5ish measures of muscle thickness. Filtering down from 1 to 3 lifts (adding two additional conditions) took our potential pool of lifters down from about 2,250 to 30. Adding another seven or eight conditions would probably wipe it out entirely.
Thus, when we estimate that Barbalho would need to be surrounded by a population of 70,000 male lifters, and he would need to test 13,000 lifters to recruit 30 sufficiently homogeneous subjects for just one of his studies, that should be interpreted as a lower bound that’s almost implausibly charitable.
Other Findings
That concludes the data anomalies that made it into the white paper. We wanted to include the “greatest hits” in the white paper – findings that were quantifiably strong. However, we’ve come across several other little quirks whose probabilities are either harder to quantify or unquantifiable.
Starting with productivity, Barbalho has published 14 first-author studies since the start of 2017, 13 of which are longitudinal studies, and we’ve been told that at least 2 more papers are either in preparation or review. Of those 16 studies, at least 4 were very ambitious, with 6-month interventions or hundreds of subjects. Most other highly productive research groups in our area have only completed 4-6 longitudinal studies in the same time frame.
It’s strange that the training protocols in Barbalho’s studies are insanely effective for increasing squat strength, but not bench press strength. The same subjects that added 51kg to their squats, jumping from 22nd to 94th percentile squatters (when compared to female powerlifters), improved their bench press strength from 30.9 to 46.3kg, training their bench in the same way they trained their squats. If they competed in powerlifting, they would have started in the 1st percentile and wound up in just the 12th percentile.
In several of these studies, strength measures and muscle thickness measures that should be correlated aren’t correlated. Quad thickness isn’t correlated with squat or knee extension strength, biceps thickness isn’t correlated with biceps curl strength, etc. One could just chalk that up as a side effect of the consistently extreme homogeneity of all measures, though (it’s hard for two variables to correlate if neither of them is “spread out” enough).
As mentioned in the intro, in the steroid study, the drug-free groups and the steroid groups were similar across all strength and muscularity measurements at baseline. The steroid groups gained way more strength and muscle during the study, though. That pair of facts only makes sense if the steroid groups were doing their first cycle during the study period. If that’s the case, that’s fine, but that’s not explained in the text of the study.
In the study on elderly females, the authors state that the subjects were block randomized, but the two groups had different numbers of subjects at baseline (203 vs. 217). Block randomization is supposed to give you two groups of approximately the same size. I’m not sure how they could perform block randomization and wind up with groups of such different sizes, unless their blocks were very large.
In some of these studies, some weeks of the training protocol seem logistically impossible. The authors will state that sets were performed to true concentric failure (until you miss a rep, and a research assistant has to help you lift the weight back up), and that each researcher was supervising groups of 5 participants. So far so good. However, during some weeks, the subjects would rest just 30-60 seconds between sets while performing sets of 12-15 reps. I’m not sure how a research assistant could simultaneously spot 5 subjects going to true failure on exercises like squat, bench press, or leg press, with the subjects resting just 30-60 seconds between sets, and doing sets of 12-15 reps. Again, there may be an explanation for this issue (e.g. a different ratio between research assistants and subjects for some training days), but it’s not provided in the text of the studies.
In one study, subjects bench pressed slightly more than they leg pressed. It’s possible that they were using a leg press model that was designed to magnify any external load several-fold, but I’ve never seen a leg press that allows people to train with lower weights than they can bench press. For that matter, leg press numbers are substantially lower than I’d expect in a lot of these studies.
As previously mentioned, one of Barbalho’s studies on trained female subjects resulted in a 33kg squat increase in 12 weeks (91.9 to 124.9kg). Another study on untrained male subjects resulted in a 15kg squat increase in 15 weeks (64.1 to 79.1kg). The training protocols were similar (6 sets to failure once per week, versus 3 sets to failure twice per week). While relative strength gains are generally similar between the sexes, absolute strength gains are generally larger for males, and untrained lifters certainly tend to gain strength substantially faster than trained lifters. It’s not clear why trained females gained more than twice as much squat strength as untrained males, over a slightly shorter time span, on comparable training programs. The male subjects were also performing conditioning, but that doesn’t strike me as a completely sufficient explanation.
On the subject of discordant strength gains between studies, in the female volume study, the subjects were trained women, and the subjects in the 5-set and 10-set groups added 42.75kg to their leg press maxes in 24 weeks (from 73.3 to 116.05kg; ~1.8kg per week). In a multi-joint vs. multi-joint plus single-joint study on untrained women, the subjects added 8.7kg to their leg press maxes in 8 weeks (from 21.2 to 29.9kg; ~1.1kg per week). Why were strength gains so much faster in the trained women who were already substantially stronger?
There are a few more nits I could pick, but I’ve hit all the high notes and most of the low notes. In closing, I want to reiterate that there may be innocent explanations for all of these statistical oddities, and I’m not trying to accuse anyone of anything. However, the explanations offered for these oddities have been sparse and (in my opinion) unconvincing so far. I’ll keep this article updated with any new developments in this saga. Until then, flip a coin for a while. Let me know when it lands on heads 30 times in a row.
Update: September 2020
A few minutes ago, we updated the white paper with new findings and developments.
As of now, no additional papers have been retracted, but we’re still in contact with the journals, and several of them are investigating the issue with the authors’ schools. You can see the updated timeline below.
IJSM indicated that they were choosing not to retract these two papers (one, two). In their email, they indicated that their decision was not final, and might change if new information came to light. We have the raw data for one of the studies, so we wanted to see if there were other anomalies in that dataset (we’ve requested data for the other study).
This was the study where, as we’ve previously noted, all subjects hip thrusted exactly 8kg more than they squatted at baseline (e.g. baseline squat and hip thrust strength were perfectly correlated; r = 1). Barbalho et al have previously reported their test-retest reliability for those two measures: r = 0.96 for hip thrust, and r = 0.98 for squat. With that in mind, we were (Andrew was) able to run a simulation to assess the likelihood of baseline squat and hip thrust 1RMs being perfectly correlated for 30 subjects, using the most charitable assumption possible (e.g. that people should hip thrust exactly 8kg more than they squat at baseline, and those measurements should be perfectly correlated). An r-value of 1 could not be replicated in 1,000,000 simulations (S > 19.9). Hence, even if we assume that it’s perfectly reasonable for there to be a “true” 8kg difference between hip thrust and squat strength, and if we assume that the “true” correlation between these two measures should be r = 1, it would still be very unlikely to observe a perfect correlation due to measurement error alone.
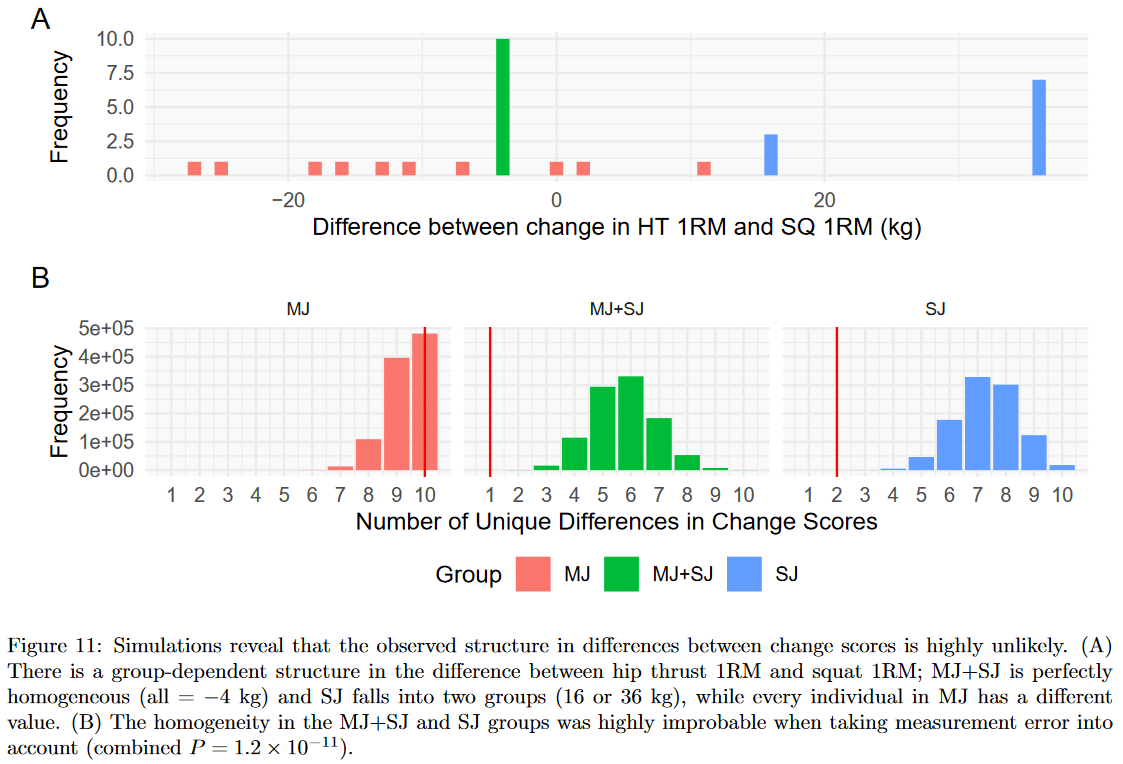
Next, we observed an unlikely pattern in the differences between squat and hip thrust change scores. All subjects in one group improved their squat by exactly 4kg more than they improved their hip thrust (perfectly homogeneous), all subjects in another group improved their hip thrust by either 16kg or 36kg more than they improved their squat (perfectly bimodal), and all subjects in the final group had unique differences between squat gains and hip thrust gains.
Since we know Barbalho et al’s reported reliability for squat and hip thrust 1RMs, Andrew was able to simulate the number of unique values that should be expected when looking at the difference between squat and hip thrust gains in each group. Again, we used very charitable assumptions (e.g. assuming that everyone in the multi-joint group should improve their squat by exactly 4kg more than they improved their hip thrust), but again, it proved to be very unlikely to observe a single repeated difference in one group and just one pair of differences in another. The combined probability of only observing one unique difference in one group and two unique differences in another was incredibly low (S = 36.3).
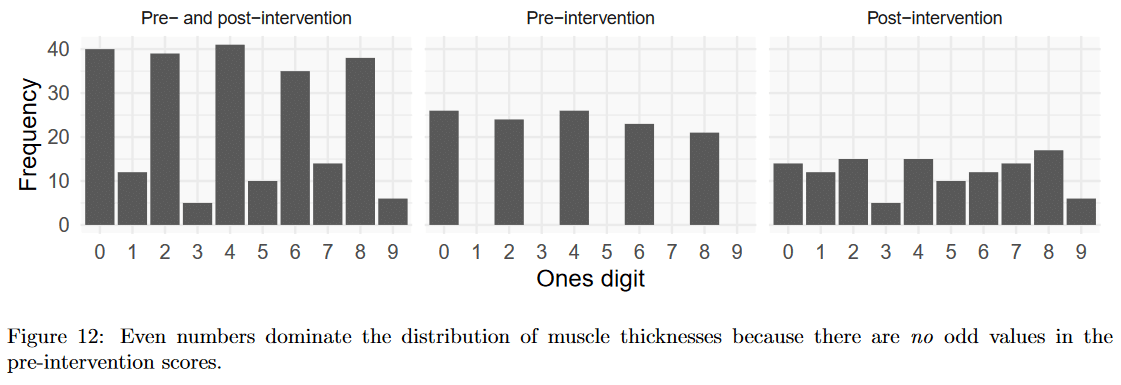
Next, we noticed a quirk in the reported muscle thicknesses. Pre-training, muscle thickness measurements were all even numbers. However, it appears that the equipment they used was capable of registering odd numbers, because approximately 40% of the post-training muscle thickness values were odd. If we assume that even and odd numbers should each show up 50% of the time for muscle thickness values, the probability of observing all even numbers for the 120 pre-training muscle thickness measures is tiny: p = 7.52 × 10-37; S = 120 (if we make the test two-sided to assess the probability of all evens OR all odds, that only bumps the S-value down to 119). Even if we assume that only 40% of numbers should be odd (using the post-training values as a point of reference), the probability of observing all even numbers for the pre-training muscle thickness measures is still tiny: 2.39 × 10-27; S = 88.4.
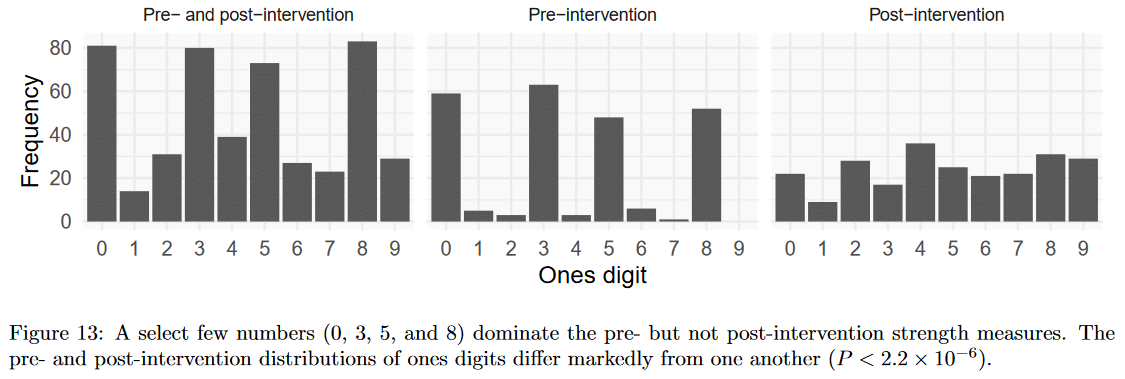
Finally, we noted that pre-training strength measures primarily ended with a 0, 3, 5, or 8, while post-training measures ended with a smoother assortment of values. The differences in these distributions are unlikely to occur by chance (S > 19.9).
That’s all for now. If there are further updates or developments, we’ll keep the white paper updated, and I’ll keep this article updated to reflect the changes in the white paper.
p.s. I’m still waiting for someone to report that they’ve gotten a fair coin to land on heads 30 times in a row.
Update, October 2020
An Expression of Concern has been published for the female volume study in MSSE.
Update, April 2021
MSSE has retracted the female volume study. You can read the full text of the retraction notification here.
Update, November 2021
JSCR has retracted the MJ/SJ study in untrained women.